 A square has an area of 30 m2. What is the length of its side?
A square has an area of 30 m2. What is the length of its side?
 John walks for one and a half hours at an average speed of 5.5 km/h.
John walks for one and a half hours at an average speed of 5.5 km/h.
Then he walks for one and a half hours at an average speed of 5 km/h.
Then he walks for one and a half hours at an average speed of 4.5 km/h.
How far does John walk?
 A curtain covers a window as shown on the right.
A curtain covers a window as shown on the right.
We approximate the area of the curtain by 2 triangles.
The area of the window is 2 square meters.
How much of the window area is covered by the curtain?
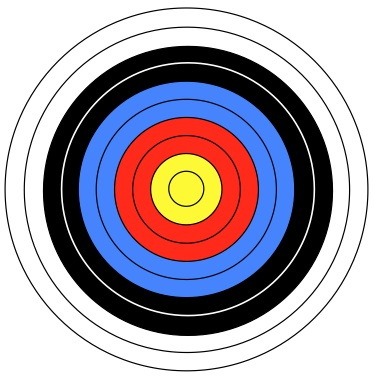 Archery target faces have five colors, with each color divided into two parts to provide scoring zones.
Archery target faces have five colors, with each color divided into two parts to provide scoring zones.
The figure shows ten concentric circles. The rings have the same width as the radius of the innermost circle.
What is the difference between the white and yellow areas?
 Which figure can be rotated 60° about its center and have its final orientation appear the same as the original orientation?
Which figure can be rotated 60° about its center and have its final orientation appear the same as the original orientation?
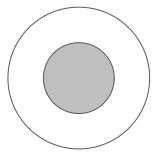 In the diagram, the radii of the two concentric circles are 5 and 10, respectively.
In the diagram, the radii of the two concentric circles are 5 and 10, respectively.
What fraction of the bigger circle is shaded?
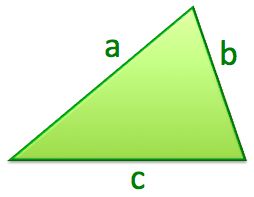 If two sides of the triangle have lengths of 11 and 22, which of the following could be the perimeter of the triangle?
If two sides of the triangle have lengths of 11 and 22, which of the following could be the perimeter of the triangle?
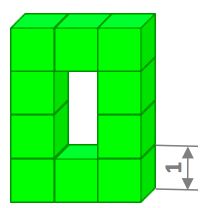 Ten cubes are glued together, and then the entire figure is painted.
Ten cubes are glued together, and then the entire figure is painted.
How many cube faces are covered in paint?
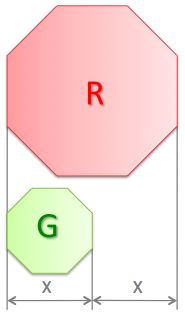 If G is the total area of the green regular octagon and R is the total area of the red regular octagon, which is correct?
If G is the total area of the green regular octagon and R is the total area of the red regular octagon, which is correct?
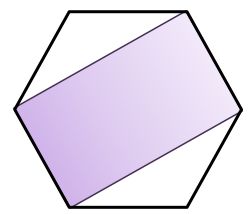 The figure shows a regular hexagon.
The figure shows a regular hexagon.
What is the fraction of the area of the colored part to the area of the entire shape?
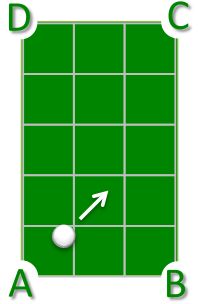 I strike a pool ball from corner A of the rectangular billiard table at an angle of 45°.
I strike a pool ball from corner A of the rectangular billiard table at an angle of 45°.
In which corner pocket will the ball fall into?
 A cross-shaped lawn has a 1-meter wide path that surrounds it.
A cross-shaped lawn has a 1-meter wide path that surrounds it.
Each side of the lawn is 5 meters in length.
What is the area of the path?
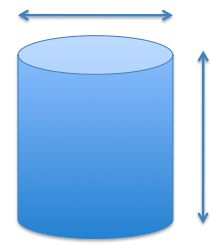 The height of a cylinder is decreased by 10%, and the radius of the cylinder is increased by 10%.
The height of a cylinder is decreased by 10%, and the radius of the cylinder is increased by 10%.
Estimate and compare the volume of the new cylinder to the first one.
 Which of these diagrams could be drawn without taking the pen off the page and without drawing along a line twice?
Which of these diagrams could be drawn without taking the pen off the page and without drawing along a line twice?
 I place a digital clock on a mirror.
I place a digital clock on a mirror.
The time 18:30 on the clock reads the same when it is reflected in the mirror.
What other time has the same property?
 This shape was formed by removing a small cube from a big cube.
This shape was formed by removing a small cube from a big cube.
The volume of the removed cube is 1/4 of the big cube's volume.
Find the surface area of the shape compared with the surface area of the big cube.
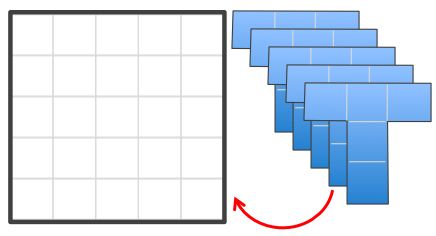 How many blue T-shapes can be placed inside the 5x5 square without intersecting each other?
How many blue T-shapes can be placed inside the 5x5 square without intersecting each other?
Find the greatest number.
 The game Battleship (Battleships or Sea Battle) is a guessing game played by two people.
The game Battleship (Battleships or Sea Battle) is a guessing game played by two people.
How many four-space battleships can you place on the 10 x 10 grid ?
Each battleship must be either vertical or horizontal, in other words not at any sort of angle.
The battleships must not touch each other, even at their corners.
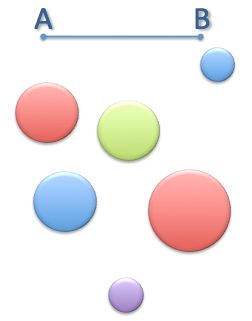 How many pairs of beads are at a distance apart which is smaller than the length of the line segment AB?
How many pairs of beads are at a distance apart which is smaller than the length of the line segment AB?
The distance between the beads is the distance between beads' centers.
 Estimate how many times larger the perimeter of the red triangle is compared with the perimeter of the blue triangle.
Estimate how many times larger the perimeter of the red triangle is compared with the perimeter of the blue triangle.
Both triangles are equilateral.
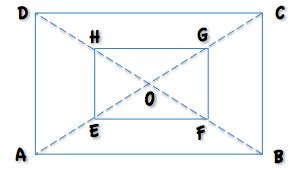 ABCD is a rectangle.
ABCD is a rectangle.
E, F, G and H are midpoints of AO, BO, CO and DO respectively.
What is the fraction of EFGH to ABCD?
Compare the perimeters.
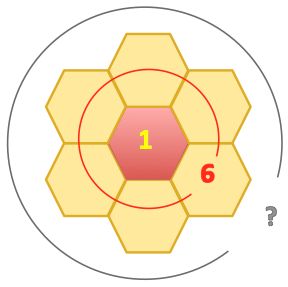 I am using red and yellow tiles to make the pattern shown on the right.
I am using red and yellow tiles to make the pattern shown on the right.
There are 6 tiles in the second 'circle'.
If I continue the pattern in the same way, how many tiles will be in the 100th "circle"?
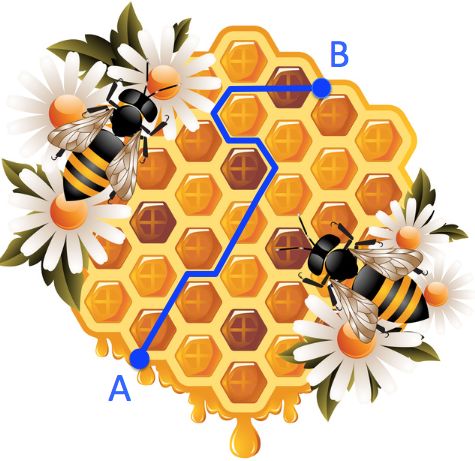 A honey bee is walking from point A to point B along the indicated path.
A honey bee is walking from point A to point B along the indicated path.
If the cells are regular hexagons with 4 mm long sides, what is the length of the path AB?
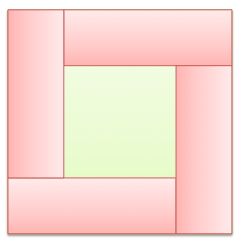 Alex is framing a small flower box by four rectangular bricks.
Alex is framing a small flower box by four rectangular bricks.
Each of the rectangles has a perimeter of 80 cm.
What is the perimeter of the entire box?
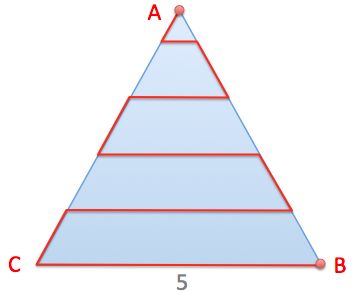 An ant goes from A to B along the indicated path in the equilateral triangle with sides that have a length of 5.
An ant goes from A to B along the indicated path in the equilateral triangle with sides that have a length of 5.
The distance between the horizontal lines is the same as the distance between point A and the first line.
The horizontal pathways are parallel to BC.
How long is the entire path?
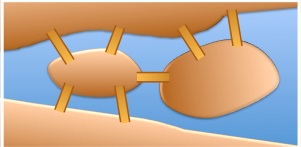 In the city of Konigsberg there were seven bridges.
In the city of Konigsberg there were seven bridges.
There was a tradition to walk and cross over each of the seven bridges.
If a young man starts and finishes at the same point, what is the smallest number of crossings he would have to make?
 How many apples can I place, such that the distance from every apple to every other apple is a single fixed value?
How many apples can I place, such that the distance from every apple to every other apple is a single fixed value?
 The volume of a box is 3000 cm3.
The volume of a box is 3000 cm3.
The ratio of the box length, width and height is
4:3:2 (length : width : height, respectively)
What could its length be?
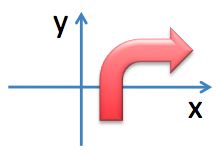 The shape is to be reflected 4 times over the vertical line y and then reflected over the horizontal line x. Find its new position.
The shape is to be reflected 4 times over the vertical line y and then reflected over the horizontal line x. Find its new position.
 Two boys, starting at the same point,
Two boys, starting at the same point,
walk in opposite directions for X meters,
turn right and walk another Y meters,
turn right and walk another X meters and then
turn right and work another Y meters.
What is the distance between them?
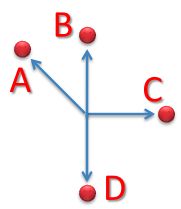 Four people start from the same point.
Four people start from the same point.
A walks northwest at 1 km/h.
B walks north at 4 km/h.
C walks east at 3 km/h.
D walks south at 1 km/h
Which people have the greatest distance between them after a one hour walk?
 John walks for one and a half hours at an average speed of 5 mph.
John walks for one and a half hours at an average speed of 5 mph.
Then he walks for one and a half hours at an average speed of 4 mph.
Then he walks for one and a half hours at an average speed of 3 mph.
How far does John walk?
 A hall is cube-shaped.
A hall is cube-shaped.
The volume of the hall is 343 cubic meters.
Find the length of a side of the floor.
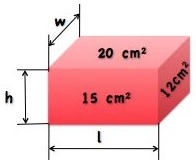 One face of a rectangular box has an area of 15 square cm. Another face is 20 square cm and the other face is 12 square cm.
One face of a rectangular box has an area of 15 square cm. Another face is 20 square cm and the other face is 12 square cm.
What is the length, l, of the box?
 One face of a rectangular box has an area of 15 square cm. Another face is 20 square cm and the other face is 12 square cm.
One face of a rectangular box has an area of 15 square cm. Another face is 20 square cm and the other face is 12 square cm.
What is the width, w, of the box?
 A school garden is 4 units long and 3 units wide.
A school garden is 4 units long and 3 units wide.
How many bushes a unit apart can be placed along the edges?
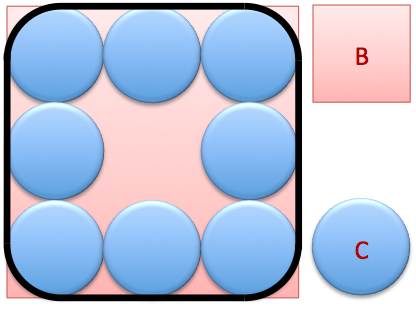 If the area of the square is B and the area of the circle is C, what is the area of the shape enclosed by the thick black line?
If the area of the square is B and the area of the circle is C, what is the area of the shape enclosed by the thick black line?
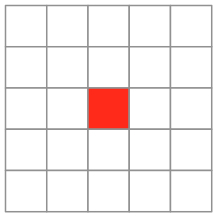 The 5 x 5 grid contains squares of different sizes from 1 x 1 to 5 x 5.
The 5 x 5 grid contains squares of different sizes from 1 x 1 to 5 x 5.
How many squares don't contain the red square?
 A set of 119 one-unit wooden cubes is packed on one level in a rectangular tray.
A set of 119 one-unit wooden cubes is packed on one level in a rectangular tray.
What is the minimum perimeter that the tray can have?
 What is the difference between the red area and the blue area if the numbers show the areas of each square?
What is the difference between the red area and the blue area if the numbers show the areas of each square?
 The border of this shape is composed of four semi-circles, each with a radius of 2 units.
The border of this shape is composed of four semi-circles, each with a radius of 2 units.
What is the area of the shape?
 I want to cut the cross by two straight cuts to make the greatest number of pieces.
I want to cut the cross by two straight cuts to make the greatest number of pieces.
What is the largest number of pieces I can get?
 What is the maximum number of points of intersection of five distinct straight lines in a plane?
What is the maximum number of points of intersection of five distinct straight lines in a plane?
This is a typical SAT question.
 Find the external surface area of the pyramid if each cube side is 1 unit.
Find the external surface area of the pyramid if each cube side is 1 unit.
Don't count the bottom and the internal surfaces.
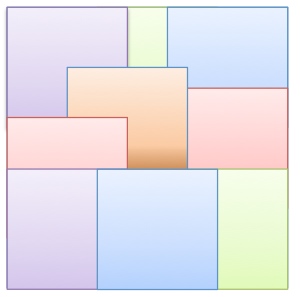 An arrangement is formed by laying nine colored squares of the same size one over another.
An arrangement is formed by laying nine colored squares of the same size one over another.
Which square is laid at the bottom?
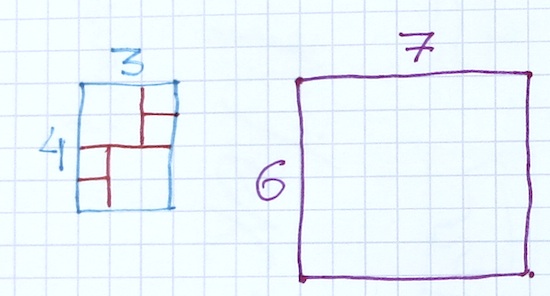 I divided a 3 x 4 square into 6 squares.
I divided a 3 x 4 square into 6 squares.
What is the smallest number of squares into which you can divide a 6 x 7 rectangle?
Author: Matt Enlow
 The sum of the perimeters of three rectangles of the same area is 172cm.
The sum of the perimeters of three rectangles of the same area is 172cm.
What is the largest possible sum of their areas?
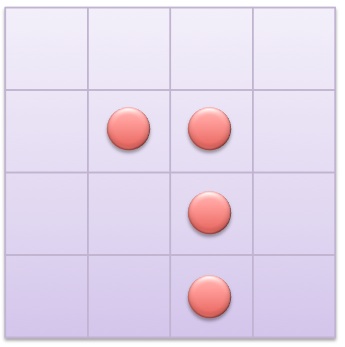 Divide the square into four equal shapes, so that each shape includes a circle.
Divide the square into four equal shapes, so that each shape includes a circle.
How many sides does the shape have?
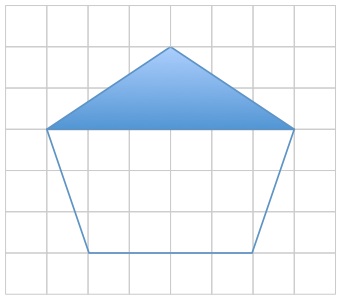 I spent 10 minutes to paint the upper part of the shape in blue.
I spent 10 minutes to paint the upper part of the shape in blue.
How much time do I need to paint the remaining part?
 I cut two or three corners off an equilateral triangle, each cut being straight.
I cut two or three corners off an equilateral triangle, each cut being straight.
What resulting shape is possible?
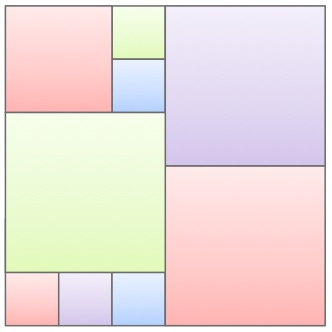 The picture shows a collection of squares. If the smallest squares have a side length of 1m, what is the area of the entire figure?
The picture shows a collection of squares. If the smallest squares have a side length of 1m, what is the area of the entire figure?
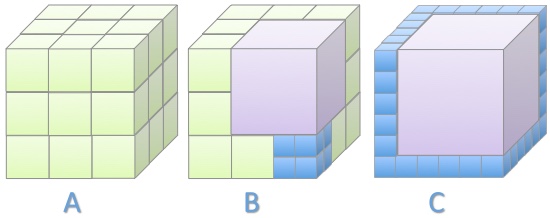 Three large cubes, which have the same sizes, are composed of smaller cubes.
Three large cubes, which have the same sizes, are composed of smaller cubes.
Which large cube contains the smaller number of cubes?
 The side length of a cube is doubled.
The side length of a cube is doubled.
What is the ratio of the old surface area of the cube to the new area of the cube, expressed as a fraction?
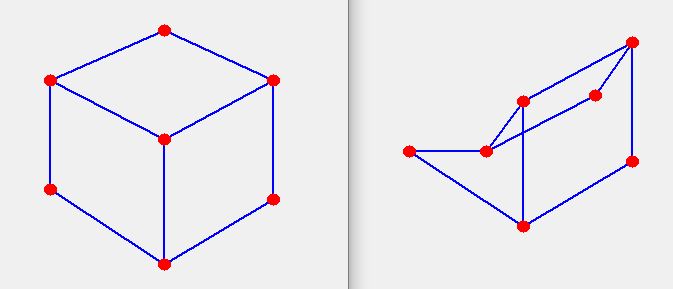 Pretend the round red blobs are tennis balls. Pretend the blue lines are stretchy strings.
Pretend the round red blobs are tennis balls. Pretend the blue lines are stretchy strings.
Can you move the tennis balls from the pattern on the left to make the pattern on the right?
NOTE: the strings are special so that whatever you do they never get tangled up with each other.
Author: Leslie Green
 An explorer finds a metal triangle on a planet.
An explorer finds a metal triangle on a planet.
His Artificial-Intelligence camera reports that two of the internal angles in the triangle are 37° and 95°.
What can you say about this triangle?
Author: Leslie Green
 An equilateral triangle contains an inscribed circle that is circumscribed around a smaller equilateral triangle.
An equilateral triangle contains an inscribed circle that is circumscribed around a smaller equilateral triangle.
If the area of the smaller triangle is 1 square meter, what the area of the yellow part of the design?
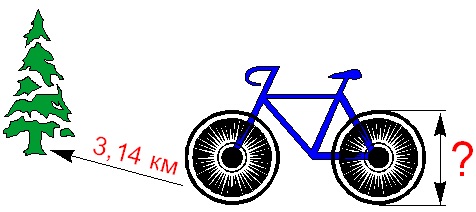 To ride the distance of 3,140 meters (3.14km), the wheel turns 1000 times.
To ride the distance of 3,140 meters (3.14km), the wheel turns 1000 times.
What is the diameter of the wheel?
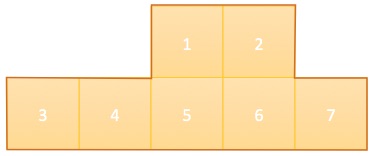 I arrange 7 unit squares to form a polygon with a perimeter of 14.
I arrange 7 unit squares to form a polygon with a perimeter of 14.
What is the minimum possible perimeter of a polygon that can be constructed with 7 unit squares?
 What is the minimum diameter of a circle that completely encloses any non-zero-area polygon with a perimeter of 10 inches?
What is the minimum diameter of a circle that completely encloses any non-zero-area polygon with a perimeter of 10 inches?
 Divide a square piece of paper into six squares with no paper remaining.
Divide a square piece of paper into six squares with no paper remaining.
What is the length of the side of the smallest square?
 Gerry divides a cube into eight equal parts using planar cuts.
Gerry divides a cube into eight equal parts using planar cuts.
The cube keeps its shape throughout the whole cutting process.
How many planar cuts are needed?
 An equilateral polygon can be concave. For example, the star is a concave decagon (ten-side polygon).
An equilateral polygon can be concave. For example, the star is a concave decagon (ten-side polygon).
What is the least number of sides a concave equilateral polygon can have?
A concave polygon has at least one internal angle greater than 180°.
An equilateral polygon has all sides of equal length, but the requirement to have all internal angles equal is only necessary for a regular polygon.
 Gerry cuts a rectangle of size 7x8 into squares with integer side lengths.
Gerry cuts a rectangle of size 7x8 into squares with integer side lengths.
What is the minimal number of squares he can get?
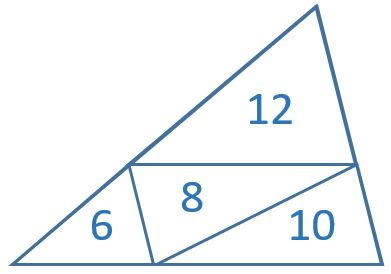 The numbers show the perimeters of the small triangles.
The numbers show the perimeters of the small triangles.
What is the perimeter of the large triangle?
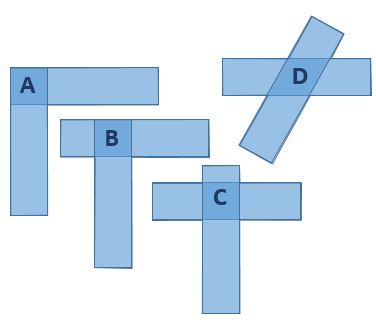 Pairs of identical rectangular strips are overlapped to form different shapes.
Pairs of identical rectangular strips are overlapped to form different shapes.
Which shape has the smallest perimeter?
 What is the minimum number of lines you need to draw (without lifting the pen from the paper) to connect the dots at the corners of a regular heptagon and the middle dot?
What is the minimum number of lines you need to draw (without lifting the pen from the paper) to connect the dots at the corners of a regular heptagon and the middle dot?
A heptagon is a seven-sided polygon or 7-gon.