 A fence around a rectangular garden has a perimeter of 14 meters.
A fence around a rectangular garden has a perimeter of 14 meters.
Its length is 4 meters.
Find the length of the diagonal of this rectangular garden.
 A fence around a rectangular garden has a perimeter of 14 meters.
A fence around a rectangular garden has a perimeter of 14 meters.
Its length is 4 meters.
Find the length of the diagonal of this rectangular garden.
 The volume of water in a glass of V cubic centimeters (cc), varies directly as its height, H centimeters (cm).
The volume of water in a glass of V cubic centimeters (cc), varies directly as its height, H centimeters (cm).
The volume is 100 cc when the height is 5 cm.
Calculate the volume when the height is 11 cm.
Note: Older text books use cubic centimeters. This unit is the same thing as cm3 and milli-liters.
1 cc = 1 cm3 = 1 mL
 Tim travels 15 meters north of the flag in the football stadium.
Tim travels 15 meters north of the flag in the football stadium.
He turns west and travels 8 meters.
He turns south and travels 6 meters and then comes back directly to the flag.
Calculate Tim's travel distance.
 A rectangle has width W, length L, and area A.
A rectangle has width W, length L, and area A.
If integer W ≤ 9 and L is an even number between 9 and 99 which of the following CANNOT be the area of the rectangle?
 A wire is wound around a circular rod.
A wire is wound around a circular rod.
The wire goes exactly 5 times around the rod.
The circumference of the rod is 12 cm and its length is 25 cm.
Identify the length of the wire.
 A boy stacked colored cubes in a square pyramid like the one shown here.
A boy stacked colored cubes in a square pyramid like the one shown here.
The top layer had 1 cube, the second layer had 4 cubes, and so on.
If the pyramid were 15 layers high, how many cubes would be in the fifteenth layer?
 A six-pointed regular star consists of two areas.
A six-pointed regular star consists of two areas.
What is the ratio of the shaded region in the area of the star?
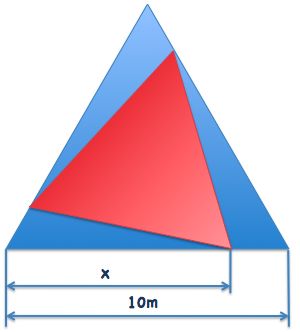 The figure shows a red equilateral triangle inscribed within another equilateral triangle. The side of the bigger triangle measures 10 meters.
The figure shows a red equilateral triangle inscribed within another equilateral triangle. The side of the bigger triangle measures 10 meters.
We want to obtain the smallest area of the red triangle. What would be the distance x in this case?
 If the volume of a cube is X cubic meters and the total surface area of the cube is X square meters, then what is the cube's edge length?
If the volume of a cube is X cubic meters and the total surface area of the cube is X square meters, then what is the cube's edge length?
 The three circles have fixed centers, and the diameter of a circle is 10% less than that of its 'left neighbor'.
The three circles have fixed centers, and the diameter of a circle is 10% less than that of its 'left neighbor'.
The left circle completes a hundred revolutions per minute.
How many revolutions does the right circle complete?
 L3 and L4 are two parallel lines in a plane.
L3 and L4 are two parallel lines in a plane.
If L3 has 3 points equally spaced along its length, and if L4 has 4 points also equally spaced along its length, how many different triangles can be formed by connecting the points on the two parallel lines?
A triangle must be formed by 2 points on one line and 1 point on the other.
 For this rectangular-faced solid (cuboid), which plane(s) contain(s) B and is/are parallel to plane AEH?
For this rectangular-faced solid (cuboid), which plane(s) contain(s) B and is/are parallel to plane AEH?
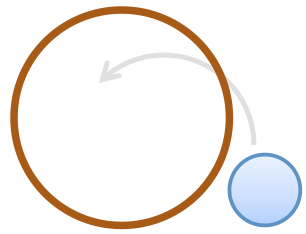
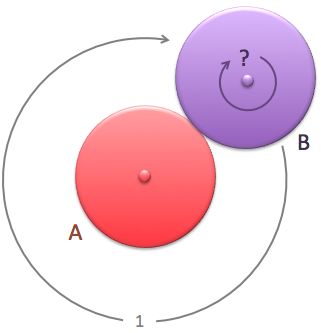 There are 2 identical circles. Circle A remains fixed, while Circle B makes 1 turn around the first one, touching it without slipping.
There are 2 identical circles. Circle A remains fixed, while Circle B makes 1 turn around the first one, touching it without slipping.
How many turns has Circle B made around its own axis?
 G is the area of the green region inside the biggest circle.
G is the area of the green region inside the biggest circle.
R is the total area of red regions of the two smaller circles.
Which statement is correct?
 The area of the external triangle is equal to 1.
The area of the external triangle is equal to 1.
Its sides' midpoints are connected to form a second triangle, and so forth.
What is the sum of the areas of all the triangles in this infinite series?
 The pattern of shading in one quarter of a square is shown in the diagram.
The pattern of shading in one quarter of a square is shown in the diagram.
If this pattern is continued indefinitely, what fraction of the large square will eventually be shaded?
 What is the maximum number of squares you can make using twelve identical matches?
What is the maximum number of squares you can make using twelve identical matches?
(The matches must not cross each other.)
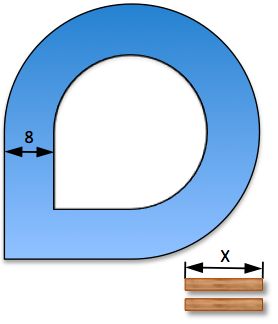 A gardener has to reach the island in the middle of a pond without getting wet.
A gardener has to reach the island in the middle of a pond without getting wet.
The gardener has two planks each X meters long.
What is the smallest length of the planks?
 Twenty matchsticks form five squares (one 3x3 and four 1x1).
Twenty matchsticks form five squares (one 3x3 and four 1x1).
How many matchsticks do I need to move to make seven squares?
Find the minimum number.
 A ladder leans against a vertical wall. The top of the ladder is 4m above the ground. When the bottom of the ladder is moved 1m closer to the wall, the top of the ladder rests 1m higher than the original position.
A ladder leans against a vertical wall. The top of the ladder is 4m above the ground. When the bottom of the ladder is moved 1m closer to the wall, the top of the ladder rests 1m higher than the original position.
How far from the wall was the bottom of the ladder in the initial position?
 If the length of the hour and minute hand of a clock are 3cm and 6cm respectively, what is the angle shown on the picture at two o'clock?
If the length of the hour and minute hand of a clock are 3cm and 6cm respectively, what is the angle shown on the picture at two o'clock?
 All inner lines connect the corners of the big square and the midpoints of the opposite sides.
All inner lines connect the corners of the big square and the midpoints of the opposite sides.
What fraction of the big square is red?
 A square is inscribed in a right triangle.
A square is inscribed in a right triangle.
Find the greatest possible ratio of the area of the square to the area of the triangle.
 The sizes of the sealed bottle with water are shown in the figure.
The sizes of the sealed bottle with water are shown in the figure.
Find the height of the water when the bottle is right side up.
 The following pattern is cut and folded to a square-based pyramid.
The following pattern is cut and folded to a square-based pyramid.
What size does the base have to be to maximize the surface area of the resulting pyramid?
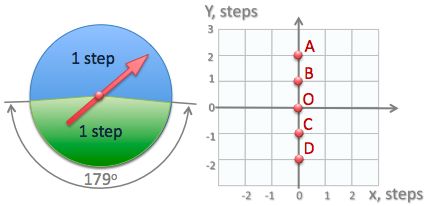 John is using the spinner shown here to define the movement.
John is using the spinner shown here to define the movement.
Blue means one step up and green means one step down.
The spinner is moved randomly.
If he starts at point 0 and makes 360 moves, where will he most likely be now?
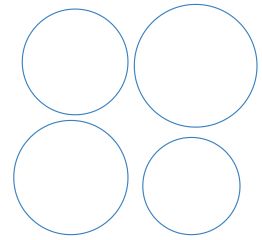 What is the maximum number of possible points of intersection of N different circles?
What is the maximum number of possible points of intersection of N different circles?
The picture shows four circles.
 Two lines trisect (divide into three equal parts) each side of the polygon ABCD.
Two lines trisect (divide into three equal parts) each side of the polygon ABCD.
Which polygon has the largest area?
 The shaded rhombus is formed by joining vertices of the square to the midpoints of its sides.
The shaded rhombus is formed by joining vertices of the square to the midpoints of its sides.
What is the area of the shaded rhombus?
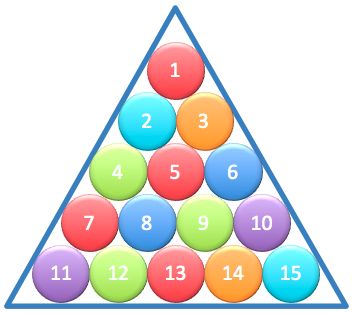 The diagram shows 15 billiard balls that fit exactly inside a triangular rack.
The diagram shows 15 billiard balls that fit exactly inside a triangular rack.
The rigid rack prevents the balls from sliding.
What is the largest number of balls that can be removed so that the remaining balls are theoretically unable to move?
 Two triangles form seven separate regions.
Two triangles form seven separate regions.
What is the greatest number of such regions that can be formed by three triangles?
 There are six ways to travel from point S to point F on a small cube if only right, forward, and up moves are permitted.
There are six ways to travel from point S to point F on a small cube if only right, forward, and up moves are permitted.
Find the number of different pathways available for a 2x2x2 cube.
 A, B, and C are squares with sides of length 1;
A, B, and C are squares with sides of length 1;
D, E, and F are isosceles right triangles;
and G is an equilateral triangle.
The net can be folded to form a shape.
What is the volume of the shape?
 I drew three lines from the center of a square that has sides with a length of 1 to form two congruent trapezoids and a pentagon.
I drew three lines from the center of a square that has sides with a length of 1 to form two congruent trapezoids and a pentagon.
All three shapes have the same area.
What is the length of the pentagon's shortest side?
 What is the maximum number of pieces that an apple can be divided into with four straight planar cuts?
What is the maximum number of pieces that an apple can be divided into with four straight planar cuts?
The pieces do not move.
 Each of these five circles is tangent to at least 3 others.
Each of these five circles is tangent to at least 3 others.
The medium sized circles have a radius 3.
What is the radius of the smallest green circles?
 In a city, there were seven bridges.
In a city, there were seven bridges.
There was a tradition that a newly married couple walks and crosses over each of the seven bridges only once.
If a couple starts and finishes at the same point, which city plan allows the couple to acomplish this task?
 A sphere fits inside a cube. The maximum possible ratio of the volume of the sphere to that of the cube is pi / 6, or about 0.52.
A sphere fits inside a cube. The maximum possible ratio of the volume of the sphere to that of the cube is pi / 6, or about 0.52.
If we put many small spheres inside a cube, then what is the largest possible ratio of the spheres' volume to that of the cube?
 I want to cut a wooden cube that is five inches on each side into 125 one-inch cubes.
I want to cut a wooden cube that is five inches on each side into 125 one-inch cubes.
I can do this by making 4 + 4 + 4 = 12 cuts, keeping the pieces together in the cube shape.
What is the minimum number of cuts needed if rearrangement of the pieces after each cut is allowed?
 I need 1 + 4 + 9 + 16 + 25 = 55 cubes to build a pyramid with a height of 5 cubes.
I need 1 + 4 + 9 + 16 + 25 = 55 cubes to build a pyramid with a height of 5 cubes.
Estimate the number of cubes for a pyramid with a height of 30 cubes.
 I want to place N cubes so that each cube touches every other one.
I want to place N cubes so that each cube touches every other one.
What is the largest possible N?
Inspired by Martin Gardner
 The Babylonians used a base 60 number system.
The Babylonians used a base 60 number system.
What shape inspired them to decide that a circle has 360 degrees?
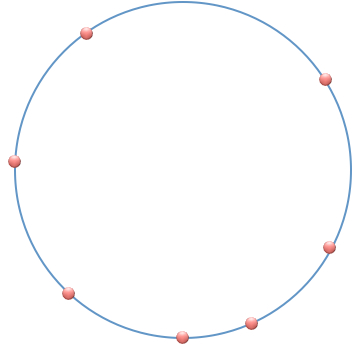 Connect N points on the circumference of a circle.
Connect N points on the circumference of a circle.
What is the largest number of intersections for the chords?
 I take a map of the city where I live and lay it on my table.
I take a map of the city where I live and lay it on my table.
There is a "You are here" point on the map, which represents the same point in the city.
The point on the map coincides with its real position.
True or False?
 I connected the midpoints of a polygon and constructed a new polygon that was a quadrilateral with opposite sides parallel.
I connected the midpoints of a polygon and constructed a new polygon that was a quadrilateral with opposite sides parallel.
What shape was the initial polygon?
 A pyramid and a tetrahedron with edges of the same length are glued together on a triangular face.
A pyramid and a tetrahedron with edges of the same length are glued together on a triangular face.
How many faces does the resulting solid have?
 I need 1 + 9 + 25 = 35 cubes to build a pyramid with a height of 3 cubes.
I need 1 + 9 + 25 = 35 cubes to build a pyramid with a height of 3 cubes.
Estimate the number of cubes for a pyramid with a height of 30 cubes.
 Inspired by Boris Kordemsky.
Inspired by Boris Kordemsky.
Four Knights problem:
Cut the chessboard into 4 congruent parts, each with a queen on it.
How many sides does each part have?
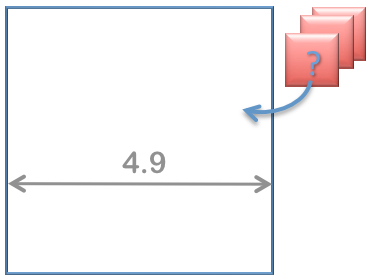 How many 1x1 squares fit into the large square with the side length 4.8?
How many 1x1 squares fit into the large square with the side length 4.8?
Find the maximum possible number.
 The picture shows three squares with the side lengths of 10, 8, and 4 cm.
The picture shows three squares with the side lengths of 10, 8, and 4 cm.
What is the difference between the areas of the green and blue regions?
 A trapezoid is formed by cutting off the top part of an isosceles right triangle such that the short base is 8 m.
A trapezoid is formed by cutting off the top part of an isosceles right triangle such that the short base is 8 m.
What is the area of the blue trapezoid?
 A circle goes through two adjacent vertices of a square and it is tangent to the bottom side of the square.
A circle goes through two adjacent vertices of a square and it is tangent to the bottom side of the square.
Find the diameter of the circle X.
 A helicopter takes me from Lausanne, Switzerland to the Swiss capital Bern in 20 minutes. Bern is 36 minutes from Brig.
A helicopter takes me from Lausanne, Switzerland to the Swiss capital Bern in 20 minutes. Bern is 36 minutes from Brig.
Which of the following could be the time of a flight from Lausanne to Brig?
 What is the probability of breaking a stick into three pieces and forming a triangle?
What is the probability of breaking a stick into three pieces and forming a triangle?
The pieces must intersect at their tips to form the triangle.
 What is the maximum number of trees that can be planted, not closer than 3 meters apart, in a square plot of 10.5 meters x 10.5 meters?
What is the maximum number of trees that can be planted, not closer than 3 meters apart, in a square plot of 10.5 meters x 10.5 meters?
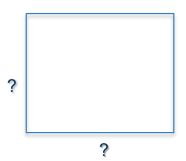 A rectangular yard with an area of 24 m2 has sides in the ratio 2:3.
A rectangular yard with an area of 24 m2 has sides in the ratio 2:3.
What is the length of the fence around the yard?
 The size of an NBA basketball court is about 29 by 16 meters.
The size of an NBA basketball court is about 29 by 16 meters.
How many courts can be planned in an 80 x 67 meter school yard, given that at least 3 meters must separate the courts?
 The golden border of the hexagonal brooch with maximum size 60 mm includes a gemstone, whose maximum size is 40 mm.
The golden border of the hexagonal brooch with maximum size 60 mm includes a gemstone, whose maximum size is 40 mm.
Which area is the largest?
 What is the maximum number of sections into which a pancake may be divided by four straight cuts through it?
What is the maximum number of sections into which a pancake may be divided by four straight cuts through it?
(NOTE: The pieces cannot be re-arranged between cuts.)
 If I use 30 g of batter to make a crêpe of 30 cm in diameter, how much batter do I need for a square pancake of the same thickness and with a side length of 30 cm?
If I use 30 g of batter to make a crêpe of 30 cm in diameter, how much batter do I need for a square pancake of the same thickness and with a side length of 30 cm?
"Archaeological evidence suggests that pancakes are probably the earliest and most widespread cereal food eaten in prehistoric societies." - Wikipedia
 The picture shows a large cube 4 x 4 x 4 that was assembled from one-unit cubes.
The picture shows a large cube 4 x 4 x 4 that was assembled from one-unit cubes.
It will be painted on all 6 sides.
For what size of large cube will the total number of painted faces of the small cubes be equal to the number of unpainted faces?
 What is the largest number of straight lines you can draw through 9 points, so that each line goes exactly through 3 points?
What is the largest number of straight lines you can draw through 9 points, so that each line goes exactly through 3 points?
You can move points on the plane as you wish.
 John cuts a large piece of cheese into small pieces using straight cuts from a very sharp cheese wire.
John cuts a large piece of cheese into small pieces using straight cuts from a very sharp cheese wire.
He does not move the pieces from the original shape while he cuts the cheese.
How many small pieces of cheese can he get using only five cuts?
 Gerry has 24 meters of fence and wants to make a rectangular garden with the largest area.
Gerry has 24 meters of fence and wants to make a rectangular garden with the largest area.
He uses the house as the fourth side of the garden.
What length should he make the long side of the garden?
 Take two sheets of A4 paper (210 x 297 millimeters or 8.3 x 11.7 inch).
Take two sheets of A4 paper (210 x 297 millimeters or 8.3 x 11.7 inch).
Roll one into a short cylinder and the other into a tall cylinder.
Which one holds more air than the other?
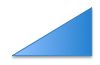 Two right-angled triangles have integer side lengths.
Two right-angled triangles have integer side lengths.
Whilst all of the sides have different lengths, the hypotenuses are equal.
What is the smallest length of the hypotenuse?
 Estimate the maximum number of smaller 1-inch circles that fit in a larger circle, the diameter of which is three times larger.
Estimate the maximum number of smaller 1-inch circles that fit in a larger circle, the diameter of which is three times larger.
 My garden fence creates a ten meters by five meters rectangle.
My garden fence creates a ten meters by five meters rectangle.
If I reuse all of this fencing to make a new rectangular garden, what is the maximum possible percentage increase of the area?
 Three semicircles are constructed on the hypotenuse and legs of a right angle triangle.
Three semicircles are constructed on the hypotenuse and legs of a right angle triangle.
Compare green (G) and red (R) areas.
 There are 3 circles of equal diameter.
There are 3 circles of equal diameter.
A line is tangent to the third circle, as shown.
Find the length of the line segment AB.
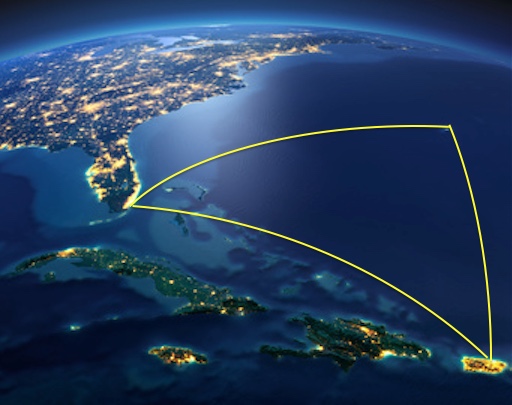 The Bermuda Triangle, also known as the Devil's Triangle, is a loosely defined region, where a number of aircraft and ships are said to have disappeared under mysterious circumstances. The triangle's three vertices are in Miami, Florida peninsula; in San Juan, Puerto Rico; and in the mid-Atlantic island of Bermuda.
The Bermuda Triangle, also known as the Devil's Triangle, is a loosely defined region, where a number of aircraft and ships are said to have disappeared under mysterious circumstances. The triangle's three vertices are in Miami, Florida peninsula; in San Juan, Puerto Rico; and in the mid-Atlantic island of Bermuda.
The distance from Miami to Bermuda is 1668 km.
The distance from Miami to Puerto Rico is 1663 km.
The distance from Puerto Rico to Bermuda is 1571 km.
Estimate the surface area of the famous triangle.
 A farmer has 36-meter of fence to enclose a field. The fence is given as 6-meter straight sections.
A farmer has 36-meter of fence to enclose a field. The fence is given as 6-meter straight sections.
He wants to make his field as big as possible.
Estimate the maximum area of his field.
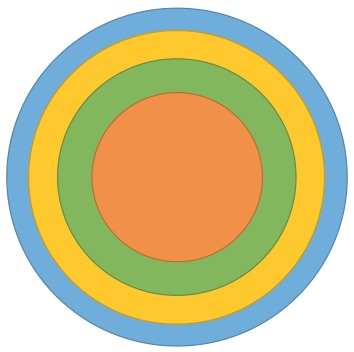 All the circles have the same center. The area of each colored region between the circles is equal to the area of the smaller circle.
All the circles have the same center. The area of each colored region between the circles is equal to the area of the smaller circle.
We extend the model to 100 circles.
How much larger is the largest circle compared to the small circle?
 The picture shows two regular stars with heights of length 1 and 3, which have the same vertical axis of symmetry.
The picture shows two regular stars with heights of length 1 and 3, which have the same vertical axis of symmetry.
What fraction of the design is blue?
 What is the ratio of sides of a circumscribed regular hexagon to an inscribed regular hexagon sharing the same circle (as shown in the picture)?
What is the ratio of sides of a circumscribed regular hexagon to an inscribed regular hexagon sharing the same circle (as shown in the picture)?
Author: Leslie Green
 The ball is covered with hexagons and pentagons.
The ball is covered with hexagons and pentagons.
The sum of interior angles of a hexagon on a plane is 720°.
What is the sum of the interior angle of the hexagon on the ball's surface?
 The ball's design stitches together 20 hexagons with 12 pentagons for a total of 32 panels. The ball made its World Cup debut as Adidas' Telstar in 1970 in Mexico. The ball's pattern of white hexagons with black pentagons made it easily visible on television.
The ball's design stitches together 20 hexagons with 12 pentagons for a total of 32 panels. The ball made its World Cup debut as Adidas' Telstar in 1970 in Mexico. The ball's pattern of white hexagons with black pentagons made it easily visible on television.
FInd the sum of the internal angles of the panels.
 A drop of paint falls onto a horizontal flat sheet of clean glass. We suppose that at a particular instant the drop forms a perfect sphere in the air. The paint has spread out into a uniform circular disc (disk) of a diameter that is twice as large as the initial sphere diameter.
A drop of paint falls onto a horizontal flat sheet of clean glass. We suppose that at a particular instant the drop forms a perfect sphere in the air. The paint has spread out into a uniform circular disc (disk) of a diameter that is twice as large as the initial sphere diameter.
What is the ratio of the disc thickness, t to the initial diameter of the drop?
Author: Leslie Green
 I cut a net from a square sheet of paper to form a cylinder A.
I cut a net from a square sheet of paper to form a cylinder A.
I cut two nets from the identical sheet to forms 2 small cylinders B.
Compare the volumes of the two sets.
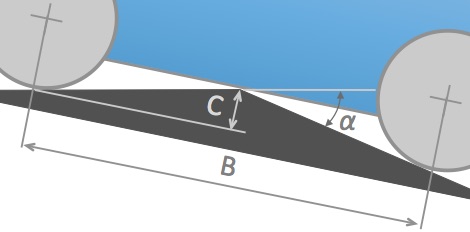 The ground clearance (C) is measured between the flat ground and the lowest point in the vehicle's undercarriage.
The ground clearance (C) is measured between the flat ground and the lowest point in the vehicle's undercarriage.
The wheel base (B) is measured between the centers of the two wheels.
The Breakover Angle (A) is an angle that a vehicle can drive over without the ground touching the vehicle's undercarriage.
What is the formula for the Breakover Angle?
 Pretend the round red blobs are tennis balls. Pretend the blue lines are stretchy strings.
Pretend the round red blobs are tennis balls. Pretend the blue lines are stretchy strings.
Can you move the tennis balls from the pattern on the left to make the pattern on the right?
NOTE: the strings are special so that whatever you do they never get tangled up with each other.
Author: Leslie Green
 Pretend the round red blobs are tennis balls. Pretend the blue lines are stretchy strings.
Pretend the round red blobs are tennis balls. Pretend the blue lines are stretchy strings.
Can you move the tennis balls from the pattern on the left to make the pattern on the right?
NOTE: the strings are special so that whatever you do they never get tangled up with each other.
Author: Leslie Green
 Leslie Green asks:
Leslie Green asks:
Which of these graphs is the sine function?
(HINT: Look at the inset picture which shows how the sine function relates to a right-angled triangle.)
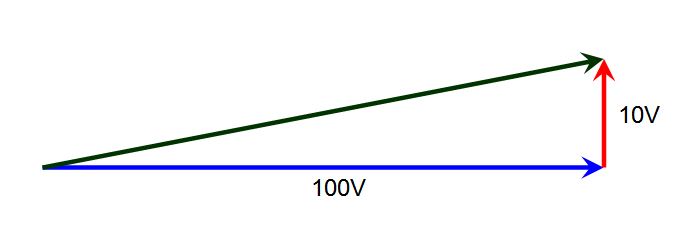 Sine waves are fascinating things. The slope of a sine wave is another sine wave, just shifted in time (phase). You can also add two sinusoidal waves, each of which has a different amplitude and a different zero crossing point (phase) and still end up with a sine wave. Furthermore, the addition of these sine waves obeys the rules of vectors (but using phase instead of direction) so you can draw a triangle and calculate the resulting amplitude and phase from that.
Sine waves are fascinating things. The slope of a sine wave is another sine wave, just shifted in time (phase). You can also add two sinusoidal waves, each of which has a different amplitude and a different zero crossing point (phase) and still end up with a sine wave. Furthermore, the addition of these sine waves obeys the rules of vectors (but using phase instead of direction) so you can draw a triangle and calculate the resulting amplitude and phase from that.
In the picture we are adding a 100V sine wave to a 10V sine wave which is phase shifted by 90° relative to the larger voltage.
What is the amplitude of the resultant sine wave?
Author: Leslie Green
 John is in the wilderness and encounters a fast flowing river. There is only one spot to cross as the bank is very steep, except at this one point. Directly across from this point is another break in the bank, with no other breaks visible. He therefore has to swim directly across the river.
John is in the wilderness and encounters a fast flowing river. There is only one spot to cross as the bank is very steep, except at this one point. Directly across from this point is another break in the bank, with no other breaks visible. He therefore has to swim directly across the river.
With his back-pack he can swim at 1 m/s in still water. The river is flowing at 0.8m/s. It is 12 m across the river.
How long does it take him to cross the river, swimming with his normal amount of effort?
Author: Leslie Green
 Leslie Green asks:
Leslie Green asks:
For a small angle d (in radians), the sine of the angle is approximately equal to the angle.
Often the cosine of a small angle is approximated as 1.
Which is the best approximation for the cosine of this small angle?
(Hint: Pythagoras)
 A piece of wood is a square with a right-angled isosceles triangle on top.
A piece of wood is a square with a right-angled isosceles triangle on top.
A carpenter cuts it to form a square tabletop with no pieces left over.
What is the minimum number of saw cuts?
Source: Alex van den Branhof, Jan Guichelaar, Arnout Jaspers Half a Century of Pythagoras Magazine. MAA 2011
 How many different convex pentagons with the vertexes in 5 of these 8 points can be formed?
How many different convex pentagons with the vertexes in 5 of these 8 points can be formed?
A convex polygon is a simple polygon (not self-intersecting) in which no line segment between two points on the boundary ever goes outside the polygon. For example, a regular hexagon is a convex polygon, while a star is not convex.
 Pretend the round red blobs are tennis balls. Pretend the blue lines are stretchy strings.
Pretend the round red blobs are tennis balls. Pretend the blue lines are stretchy strings.
Can you move the tennis balls from the pattern on the left to make the pattern on the right?
NOTE: the strings are special so that whatever you do they never get tangled up with each other.
Author: Leslie Green
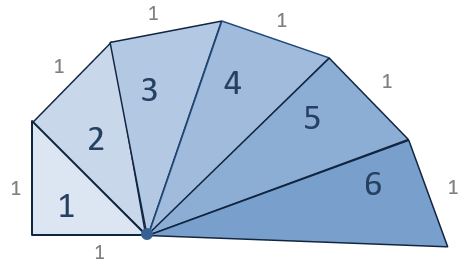 The spiral of Theodorus (also called Pythagorean spiral) is a spiral composed of contiguous right triangles.
The spiral of Theodorus (also called Pythagorean spiral) is a spiral composed of contiguous right triangles.
Which triangle has an area of 10?
 A regular hexagon with a side length 1 can be decomposed into six regular triangles with the same side length.
A regular hexagon with a side length 1 can be decomposed into six regular triangles with the same side length.
Which is the only other regular polygon with unit side lengths which can be decomposed into smaller regular triangles and squares with sides of length 1?
 Cut a square paper into acute triangles.
Cut a square paper into acute triangles.
What is the smallest possible number of the triangles?
An acute triangle has all angles smaller than a right angle (90°).
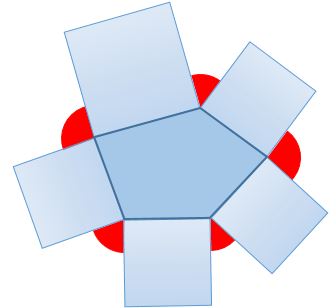 I draw different polygons, and then I construct squares on the outside of each polygon, using the whole of each polygon side.
I draw different polygons, and then I construct squares on the outside of each polygon, using the whole of each polygon side.
For example, the picture shows a pentagon with the squares.
I count the sum of the marked angles between the squares.
For what polygon is the sum of the gap angles largest?
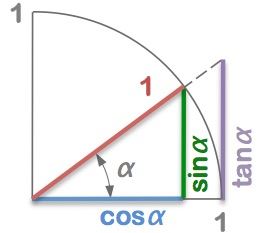 Leslie Green asks:
Leslie Green asks:
Given that the cosine of an angle is 3/5, find the sine of that angle without using a calculator or trig tables.
Hint: use Pythagoras.
 A cube has a green face, two yellow faces, and three red faces.
A cube has a green face, two yellow faces, and three red faces.
How many different such cubes can I make?
Two cubes are different if one cube cannot be rotated to look like the other.
 Three lines define seven separate regions.
Three lines define seven separate regions.
What is the maximum number of regions divided by six lines in the plane?
 A diagonal divides a large square into two triangles.
A diagonal divides a large square into two triangles.
How much larger is the area of the yellow square compared to the area of the green square?