 A rectangle has a width of 0.3x and a length of 0.4x.
A rectangle has a width of 0.3x and a length of 0.4x.
Which formula is the correct one to calculate the perimeter (P) in terms of x?
 A rectangle has a width of 0.3x and a length of 0.4x.
A rectangle has a width of 0.3x and a length of 0.4x.
Which formula is the correct one to calculate the perimeter (P) in terms of x?
 The edges of a large cube are 3 times longer than the edges of a small cube.
The edges of a large cube are 3 times longer than the edges of a small cube.
How many times greater is the volume of the large cube than the small cube?
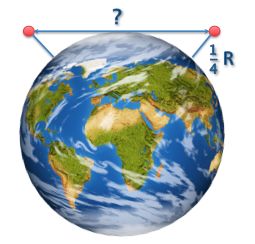 Two satellites orbit at 1/4 R above Earth's surface. R is the radius of the Earth.
Two satellites orbit at 1/4 R above Earth's surface. R is the radius of the Earth.
What is the maximum distance at which the two satellites can see each other?
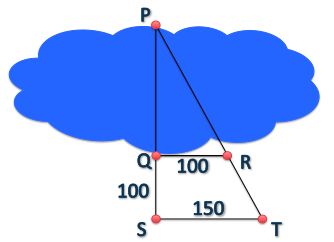 A mathematician wants to approximate the width of a lake.
A mathematician wants to approximate the width of a lake.
He places 5 markers near the lake and measures the distances shown in the diagram.
What is the width of the lake in meters (m) from point P to point Q?
 A square garden is 401 square meters.
A square garden is 401 square meters.
The minimum distance between apple trees is 5 meters. The minimum distance between a tree and the fence around the garden is 5 meters.
What is the maximum number of trees that can fit in the garden?
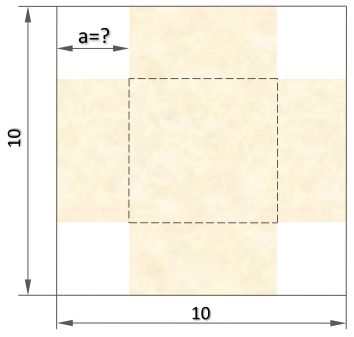 A boy is making boxes from cardboard.
A boy is making boxes from cardboard.
He is going to cut square pieces off each corner as shown in the diagram and fold the sides up.
Which size of square pieces would give a larger box in terms of volume?
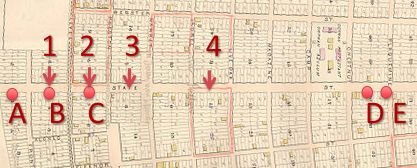 Five boys Andrew, Brandon, Chris, Daniel, and Ethan live on State Street.
Five boys Andrew, Brandon, Chris, Daniel, and Ethan live on State Street.
At which point should the children meet so that the sum of the distances they walk to that point is minimized?
 A boy cuts a cardboard circle and only cuts 5 straight lines.
A boy cuts a cardboard circle and only cuts 5 straight lines.
He does not care if the pieces are equal.
What is the maximum number of pieces he can obtain if he makes 5 cuts without moving the cut pieces?
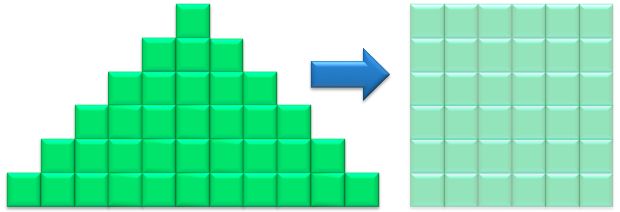 The figure shows a pyramid made of small squares.
The figure shows a pyramid made of small squares.
I want to move the small squares and transform the pyramid into a big square.
What is the lowest possible number of moves that need to be made?
 The American flag consists of thirteen equally spaced, horizontal red and white stripes, with a blue rectangle in the canton bearing fifty small, white, five-pointed stars.
The American flag consists of thirteen equally spaced, horizontal red and white stripes, with a blue rectangle in the canton bearing fifty small, white, five-pointed stars.
What part of the flag is red?
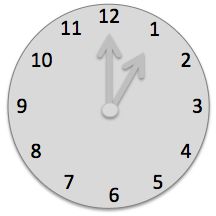 Divide the analog watch face with two straight lines so that the sums of the numbers in each part are equal.
Divide the analog watch face with two straight lines so that the sums of the numbers in each part are equal.
Which is true?
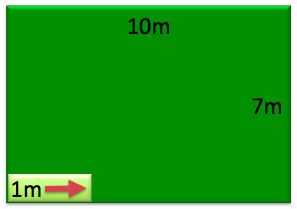 Bill mows the front lawn, which is a 7m by 10m rectangle.
Bill mows the front lawn, which is a 7m by 10m rectangle.
The mower cuts a 1m wide strip.
If Bill starts at the corner and mows around the lawn in a spiral toward the center, how many times around must he go before he has mowed the lawn?
 The blocks of ice are of the same height and depth.
The blocks of ice are of the same height and depth.
Find the picture of the heaviest block (or set of blocks).
 A block of wood in the form of a cuboid 9 x 10 x 11 has all its six faces painted red.
A block of wood in the form of a cuboid 9 x 10 x 11 has all its six faces painted red.
If the wooden block is cut into small cubes of 1 x 1 x 1, how many of these cubes would have red paint on them?
 I fold a square piece of paper in half four times without unfolding, making an isosceles right triangle each time.
I fold a square piece of paper in half four times without unfolding, making an isosceles right triangle each time.
What is the correct net of the creases on the paper after unfolding the paper?
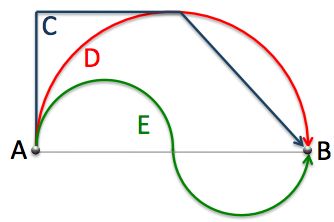 Path C consists of straight segments.
Path C consists of straight segments.
Path D and E consist of semi-circles.
Which path is the longest?
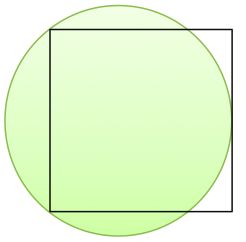 A circle is drawn through two vertices of a square so that it is tangent to one side of the square.
A circle is drawn through two vertices of a square so that it is tangent to one side of the square.
The square has sides of length 8.
Find the radius of the circle.
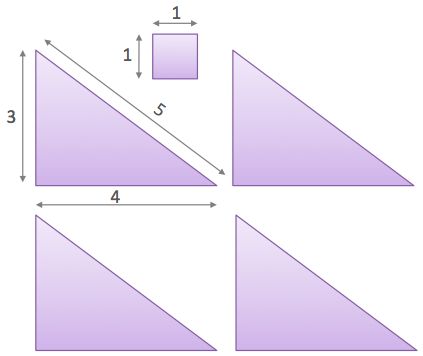 I placed together four identical triangles and the square, without overlaps, to form a figure.
I placed together four identical triangles and the square, without overlaps, to form a figure.
What is the least possible perimeter of the new figure?
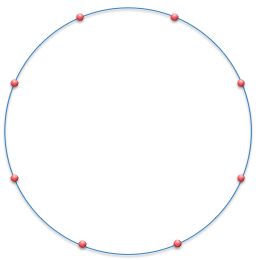 Eight points are equally spaced on a circle.
Eight points are equally spaced on a circle.
How many right angled triangles that have all their vertices at three of these points can you draw?
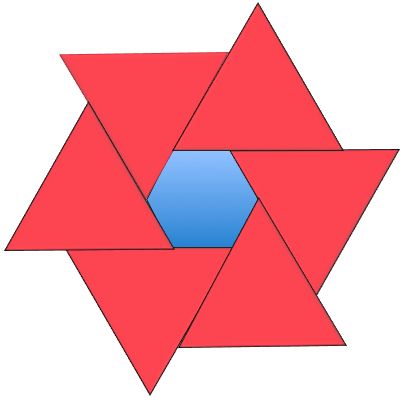 The picture shows six equilateral triangles.
The picture shows six equilateral triangles.
The sides of the triangles are three times longer than the sides of the regular hexagon.
What fraction of the whole shape is blue?
 The picture shows a tiling pattern which is made of square green tiles 10 x 10 cm and gray tiles 20 x 10 cm.
The picture shows a tiling pattern which is made of square green tiles 10 x 10 cm and gray tiles 20 x 10 cm.
The pattern is extended to cover a large surface.
What fraction of the surface is colored green?
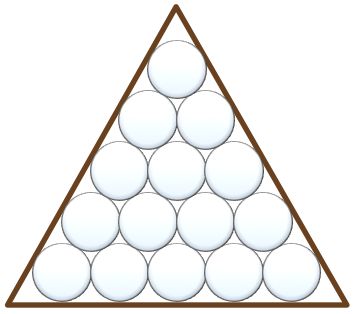 Fifteen billiard balls perfectly fit into a triangular rack.
Fifteen billiard balls perfectly fit into a triangular rack.
What is the largest number of the balls that fit into the rack when its side lengths are decreased by 20%?
 What is the smallest number of segments that needs to be moved so that the pattern has a line of symmetry?
What is the smallest number of segments that needs to be moved so that the pattern has a line of symmetry?
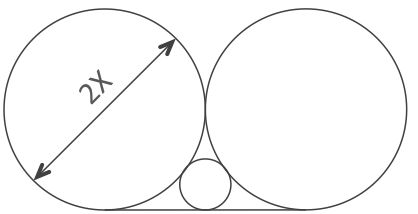 All three circles are tangent to the horizontal line and to one another.
All three circles are tangent to the horizontal line and to one another.
The diameter of the small circle is 2.
Find the diameter of the big circles.
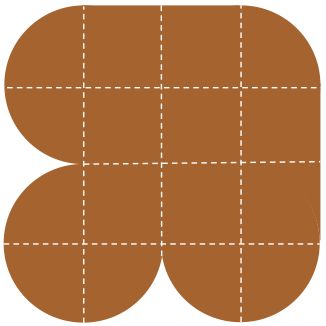 A girl wants to cut the paper into several equal pieces of the same shape, and with nothing left over.
A girl wants to cut the paper into several equal pieces of the same shape, and with nothing left over.
(NOTE: She does not have to cut along the dotted lines.)
How many pieces are possible?
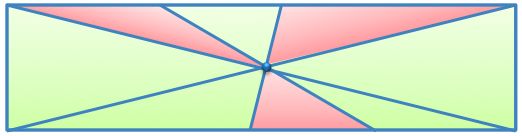 Two lines and two diagonals are drawn through the center of the rectangle.
Two lines and two diagonals are drawn through the center of the rectangle.
What fraction of the area of the rectangle is green?
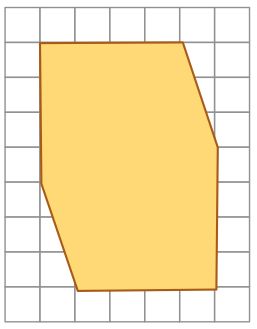 I would like to cut the shape into the fewest possible pieces that will fit together and form a rectangle.
I would like to cut the shape into the fewest possible pieces that will fit together and form a rectangle.
What is the smallest number of pieces?
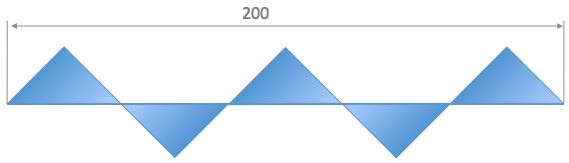 The colored figure in the picture consists of isosceles right triangles.
The colored figure in the picture consists of isosceles right triangles.
What is the largest possible area of the blue shape?
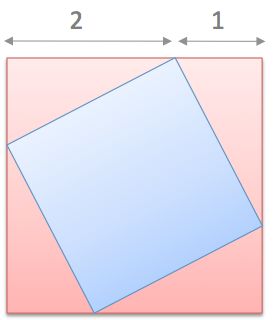 The vertices of the smaller square divide each side of the larger square by a ratio of 2:1.
The vertices of the smaller square divide each side of the larger square by a ratio of 2:1.
What fraction of the larger square is blue?
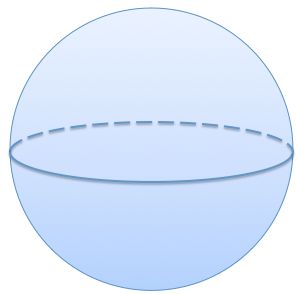 I blew some air into a spherical balloon and quadrupled its surface area (4 times).
I blew some air into a spherical balloon and quadrupled its surface area (4 times).
By how much did I multiply the volume of the sphere?
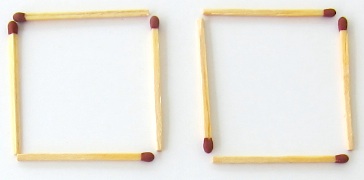 Four matchsticks form a square.
Four matchsticks form a square.
How many non-overlapping squares can be formed using eight matchsticks?
Note: The matchsticks do not intersect each other.
 What is the maximum number of apples (ideal spherical units) that can touch another given apple (spherical unit) without overlapping?
What is the maximum number of apples (ideal spherical units) that can touch another given apple (spherical unit) without overlapping?
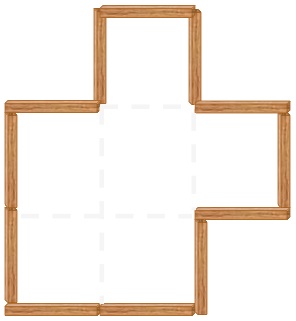 I arranged twelve one-inch wooden sticks in a polygon with an area of 6 square inches.
I arranged twelve one-inch wooden sticks in a polygon with an area of 6 square inches.
I would like to form a polygon with an area of 4 square inches using these 12 sticks.
What is the minimum number of sides of the new polygon?
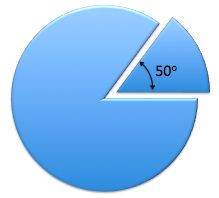 Anna has made puzzle pieces by cutting wedges from a disk.
Anna has made puzzle pieces by cutting wedges from a disk.
Each wedge cut from the disk has a 50-degree angle at the center of the disk.
The weight of the uncut disk is 108 grams.
How many grams does each 50-degree wedge weigh?
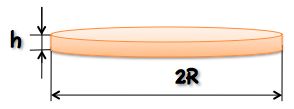 How many coins do I need to melt down and recast to get a single coin of double thickness and double diameter?
How many coins do I need to melt down and recast to get a single coin of double thickness and double diameter?
 Shape A and B are congruent equilateral triangles.
Shape A and B are congruent equilateral triangles.
Shape C is formed by superimposing shapes A and B about their centers.
What is the perimeter of shape C if the perimeter of shape A is 45 inches?
 The diagram illustrates a row of three squares formed by matches.
The diagram illustrates a row of three squares formed by matches.
How many matches will it take to make a row of 33 squares?
 A boy stacked colored cubes in a square pyramid like the one shown here.
A boy stacked colored cubes in a square pyramid like the one shown here.
The top layer had 1 cube, the second layer had 4 cubes, and so on.
If the pyramid were 16 layers high, how many cubes would be in the sixteenth layer?
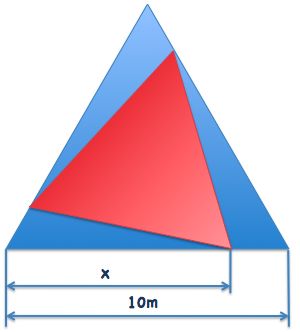 The figure shows a red equilateral triangle inscribed within another equilateral triangle. The side of the bigger triangle measures 10 meters.
The figure shows a red equilateral triangle inscribed within another equilateral triangle. The side of the bigger triangle measures 10 meters.
What is the ratio of blue area to the total area of the largest triangle?
 The three circles have fixed centers, and the diameter of a circle is 7 / 8 of its 'left neighbor'.
The three circles have fixed centers, and the diameter of a circle is 7 / 8 of its 'left neighbor'.
The left circle completes a hundred revolutions per minute.
Estimate how many revolutions the right circle completes.
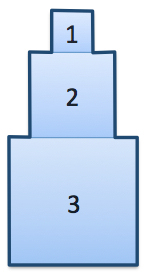 Squares 1, 2 and 3 have sides of length 1, 2 and 3 units, respectively.
Squares 1, 2 and 3 have sides of length 1, 2 and 3 units, respectively.
What is the perimeter of the entire figure if there are 100 such squares in the shape?
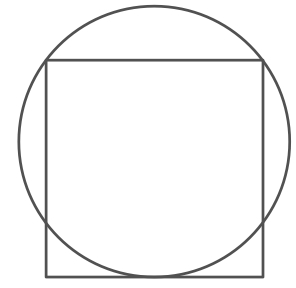 A square with a side length 20 has two vertices on the circle, and one side touching the circle.
A square with a side length 20 has two vertices on the circle, and one side touching the circle.
Find the diameter of the circle.
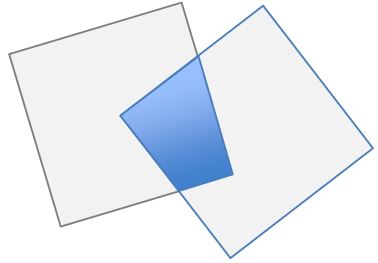 Two squares, each with sides measuring 2 cm, are placed such that a vertex of one lies at the center of the other.
Two squares, each with sides measuring 2 cm, are placed such that a vertex of one lies at the center of the other.
What is the area of the overlapping region?
 A recipe makes 5 pizzas that are 12 inches in diameter.
A recipe makes 5 pizzas that are 12 inches in diameter.
If I decide to make 3-inch diameter pizzas, how many of the smaller pizzas would this recipe make?
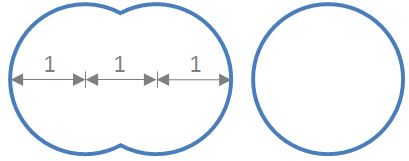 Two congruent circles share a radius.
Two congruent circles share a radius.
What is the perimeter of the figure compared with the perimeter of the original circle?
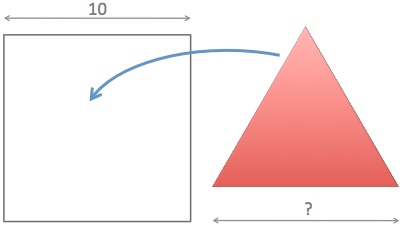 What is the largest possible side size of an equilateral triangle that fits into a square with a side size 10?
What is the largest possible side size of an equilateral triangle that fits into a square with a side size 10?
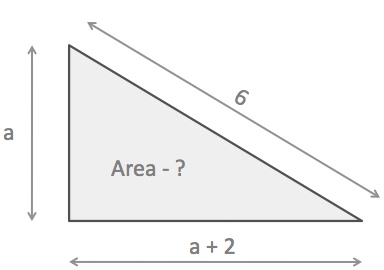 The hypotenuse of a right triangle is 6, and the length of one leg is 2 units longer than the length of the other.
The hypotenuse of a right triangle is 6, and the length of one leg is 2 units longer than the length of the other.
What’s the area of the triangle?
 What part of the rectangle is red if points A and B are the midpoints of the corresponding sides of the rectangle?
What part of the rectangle is red if points A and B are the midpoints of the corresponding sides of the rectangle?
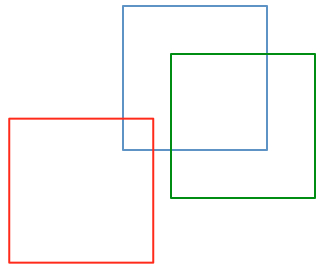 Three overlapping squares form 5 squares including themselves in the picture.
Three overlapping squares form 5 squares including themselves in the picture.
What is the greatest number of squares you can make by overlapping three squares of the same size?
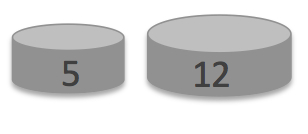 You have a 5kg weight and a 12kg weight.
You have a 5kg weight and a 12kg weight.
They are the same height and are made from the same material.
What is the ratio of their diameters?
 Estimate the maximum number of smaller 1-inch circles that fit in a larger circle, the diameter of which is 2.9 times larger.
Estimate the maximum number of smaller 1-inch circles that fit in a larger circle, the diameter of which is 2.9 times larger.
 What is the volume in cubic inches of the pyramid with height 10 inches?
What is the volume in cubic inches of the pyramid with height 10 inches?
The pyramid consists of equal cubes.
 I want to divide this shape into four congruent pieces - all of precisely the same size and shape.
I want to divide this shape into four congruent pieces - all of precisely the same size and shape.
How many sides do the four pieces have?
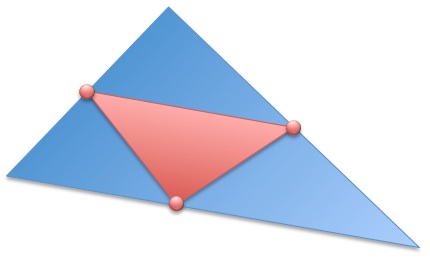 If I picked three red points, each in the middle of a different side of the big triangle, would the small triangle be similar to the big one?
If I picked three red points, each in the middle of a different side of the big triangle, would the small triangle be similar to the big one?
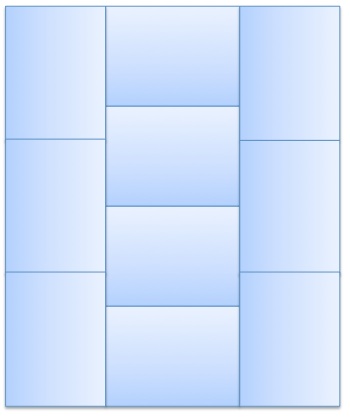 A large rectangle of perimeter 44 is divided into 10 congruent rectangles.
A large rectangle of perimeter 44 is divided into 10 congruent rectangles.
Find the perimeter of a small rectangle.
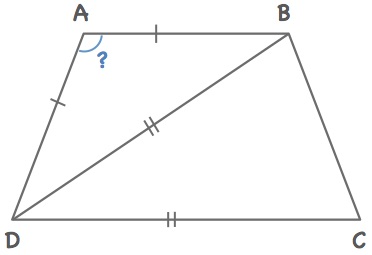 The isosceles trapezoid consists of two isosceles triangles.
The isosceles trapezoid consists of two isosceles triangles.
Isosceles means having two sides of equal length.
Find the marked angle A.
 In a triangle, the measures of the angles are in the ratio 19 : 20 : 21.
In a triangle, the measures of the angles are in the ratio 19 : 20 : 21.
What is the measure of the largest angle in the triangle?
The picture shows the Bermuda Triangle, also known as the Devil's Triangle, a loosely defined region, where a number of aircraft and ships are said to have disappeared under mysterious circumstances.
 Mars is entirely covered by land and the amount is approximately the same as the amount of land on Earth.
Mars is entirely covered by land and the amount is approximately the same as the amount of land on Earth.
29% of Earth’s surface is covered by land and 71% by water.
Approximately how many times larger is the radius of Earth compared to the radius of Mars?
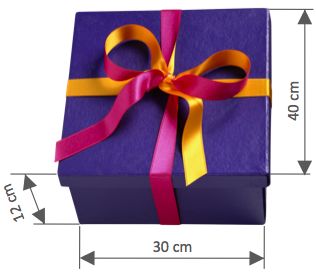 A school decided to give presents to 1000 students.
A school decided to give presents to 1000 students.
Which is the smallest room that can contain all the presents?
1m = 100cm
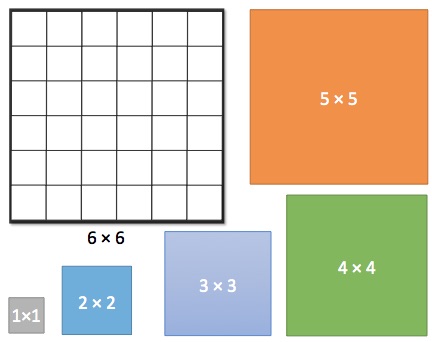 There are 15 colored squares : three squares of each color.
There are 15 colored squares : three squares of each color.
What is the largest area of the 6x6 square can be covered by the colored squares without intersection and going over?
Inspired by Knapsack problem
 "The Russian adventurer Fedor Konyukhov has broken the record for the fastest circumnavigation of the earth in a hot air balloon in 2016. The 64-year-old has beaten the late Steve Fossett’s record of circumnavigating the world by two days, making the 34,000km journey in just 11 days flying at heights of up to 10km." - The Guardian.
"The Russian adventurer Fedor Konyukhov has broken the record for the fastest circumnavigation of the earth in a hot air balloon in 2016. The 64-year-old has beaten the late Steve Fossett’s record of circumnavigating the world by two days, making the 34,000km journey in just 11 days flying at heights of up to 10km." - The Guardian.
Which extra distance would the adventurer travel if it is 12 km above the ground?
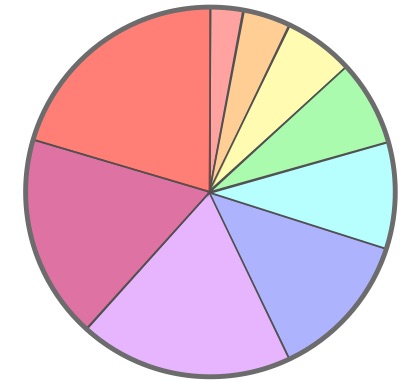 A pie chart (or a circle chart) is a circular statistical graphic, which is divided into slices to illustrate numerical proportion.
A pie chart (or a circle chart) is a circular statistical graphic, which is divided into slices to illustrate numerical proportion.
I divided my chart into 9 zones, so that the second zone is 2 times larger than the first one, the third is 3 times larger than the first one, and so on.
What is the size of the ninth zone?
 You need to find the center of a circle using only one template of a letter and a pencil.
You need to find the center of a circle using only one template of a letter and a pencil.
Which letter is the best choice?
 The diameter of the large circle is 5 times greater than the diameter of small circles (and semicircles).
The diameter of the large circle is 5 times greater than the diameter of small circles (and semicircles).
What is the ratio of the blue area to the white area inside the large circle?
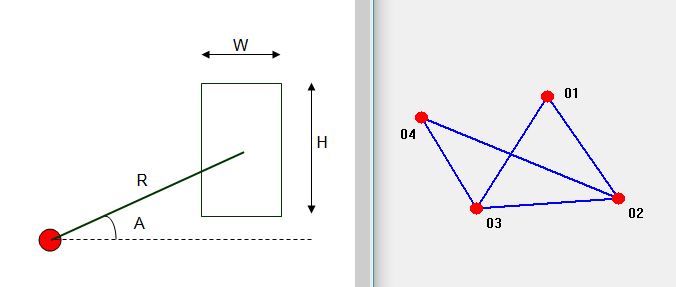
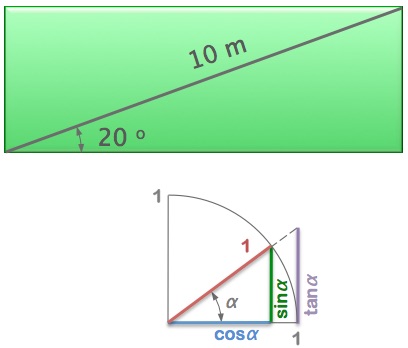 You have measured the diagonal of your rectangular lawn using a laser rangefinder onto a conveniently positioned garden gnome. You have also measured the angle of the diagonal.
You have measured the diagonal of your rectangular lawn using a laser rangefinder onto a conveniently positioned garden gnome. You have also measured the angle of the diagonal.
What is the length of the lawn?
Author: Leslie Green
 Terry the termite is taking a walk across the gap between two roses using a conveniently available cotton thread. Terry is quite good at mathematics, but not nearly as smart as his uncle Huygens. Uncle Huygens explained that the thread forms a shape known as a catenary, a curve which looks a bit like a parabola, but is more complicated than that.
Terry the termite is taking a walk across the gap between two roses using a conveniently available cotton thread. Terry is quite good at mathematics, but not nearly as smart as his uncle Huygens. Uncle Huygens explained that the thread forms a shape known as a catenary, a curve which looks a bit like a parabola, but is more complicated than that.
Terry is smart, but not that smart, so he approximates the curve as a 30° arc of a circle of radius 100mm.
What is Terry’s estimate of the (arc) length of this cotton bridge?
Author: Leslie Green
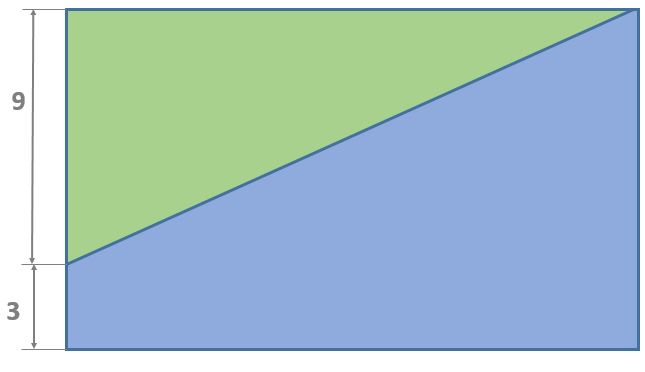 In a rectangle, the sloping line divides the area of the rectangle.
In a rectangle, the sloping line divides the area of the rectangle.
What is the ratio of green to blue area of the rectangle?
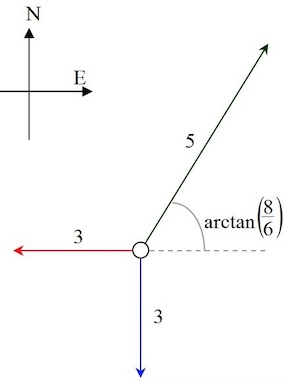 Three ropes join at a ring which is free to move relative to the ground. The forces and directions are shown at one instant.
Three ropes join at a ring which is free to move relative to the ground. The forces and directions are shown at one instant.
The sketch is not necessarily drawn to scale.
What happens next?
Author: Leslie Green
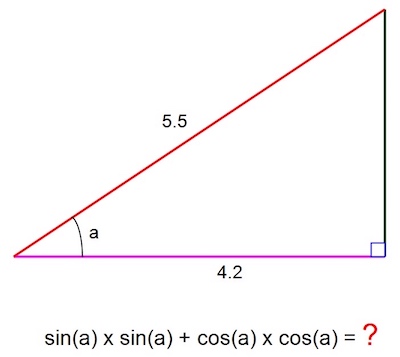 Leslie Green asks:
Leslie Green asks:
If you defined the sine and cosine functions to Pythagoras, 2500 years ago, he would easily have solved this problem.
Surely you won’t have any trouble with it?
(No cheating by using a calculator or trig tables.)
 Pretend the round red blobs are tennis balls. Pretend the blue lines are stretchy strings.
Pretend the round red blobs are tennis balls. Pretend the blue lines are stretchy strings.
Can you move the tennis balls from the pattern on the left to make the pattern on the right?
NOTE: the strings are special so that whatever you do they never get tangled up with each other.
Author: Leslie Green
 It is often said that "You cannot fit a square peg in a round hole". Obviously that is not true. Anyone with any mathematical background would use a square peg whose diagonal was equal to the diameter of the round hole.
It is often said that "You cannot fit a square peg in a round hole". Obviously that is not true. Anyone with any mathematical background would use a square peg whose diagonal was equal to the diameter of the round hole.
But we have a different question. If you bevel (cut) each corner of the square peg at a 45° angle, what is the largest cross-sectional area of peg that will fit in a circular hole of radius R?
Author: Leslie Green
 A radian is a very strange unit of angular measure. Protractors are calibrated in degrees, not radians. You will never find radians mentioned in everyday life.
A radian is a very strange unit of angular measure. Protractors are calibrated in degrees, not radians. You will never find radians mentioned in everyday life.
But computer library functions for sin(), cos() and tan() functions all use radians not degrees, so if you need to use them then you need to convert from degrees to radians. There is no need to remember the conversion factor; just work it out from first principles when you need it.
If you draw an arc with a compass, and the arc length is equal to the radius, then the angle of the arc is 1 radian.
Given that definition you should be able to calculate how many degrees make 1 radian.
Author: Leslie Green
 Did you realize that trigonometry is actually used in computer programs? The right half of the image shows a graph with node (vertex) numbers. These labels need to be rotated around the nodes in order to avoid clashing with the blue links (branches). The left half of the image shows the problem of moving the center of a text label box around a fixed point.
Did you realize that trigonometry is actually used in computer programs? The right half of the image shows a graph with node (vertex) numbers. These labels need to be rotated around the nodes in order to avoid clashing with the blue links (branches). The left half of the image shows the problem of moving the center of a text label box around a fixed point.
Assuming a standard (Cartesian) x-y co-ordinate system, and given that the node is at (Px, Py), what is the position for the top left corner of the label box?
Author: Leslie Green
 Being a bored billionaire, Martin decides to have a swimming pool built in the shape of an inverted regular tetrahedron. Of course he wasn’t sure what a tetrahedron was, so the architect explained that it is a triangular based pyramid with all four sides equal, although in this case there is no actual base because that is the surface of the water.
Being a bored billionaire, Martin decides to have a swimming pool built in the shape of an inverted regular tetrahedron. Of course he wasn’t sure what a tetrahedron was, so the architect explained that it is a triangular based pyramid with all four sides equal, although in this case there is no actual base because that is the surface of the water.
Martin is bored by the fact that the pool has taken two hours to get to a depth of one third the overall height. Filling at the same rate (in gallons per minute) he decides that it will take another 4 hours to fill completely. Everyone avoids his gaze when he makes this statement out loud.
How much longer will it really take?
Author: Leslie Green
 I cut off 4 triangles from a cross that was initially composed from 5 equal squares.
I cut off 4 triangles from a cross that was initially composed from 5 equal squares.
The height and width ratio of each triangle is 2 : 1.
Which regular shape can be composed from all these pieces if I rearrange them?
There are no superpositions.
 Jane is sitting on a bench in a museum when she sees a round coin drop from a woman's purse onto the tiled floor. She tries to guess the probability that the coin will not land on the boundary between tiles. She neglects the thickness of the boundary between the tiles and estimates that the coin diameter is one fifth the side length of the tiles. She guesses that there is a 20% chance of the coin landing on the border.
Jane is sitting on a bench in a museum when she sees a round coin drop from a woman's purse onto the tiled floor. She tries to guess the probability that the coin will not land on the boundary between tiles. She neglects the thickness of the boundary between the tiles and estimates that the coin diameter is one fifth the side length of the tiles. She guesses that there is a 20% chance of the coin landing on the border.
What is the correct probability of the coin not landing on a tile boundary?
Author: Leslie Green
 The horizontal Field of View (the size of the scene which fits into the picture) of a particular digital camera is 3m at a distance of 3m.
The horizontal Field of View (the size of the scene which fits into the picture) of a particular digital camera is 3m at a distance of 3m.
What is the angular Field of View?
(Hint: Draw a little sketch.)
Author: Leslie Green
 The blue ball weighs somewhere between 1 and 31 times the weight of a red ball, the ratio being an integer. Enough red balls are placed on the right hand side of the balance to make the beam level. The minimum number of red balls is used to balance any particular weight. There is no restriction on the number of balls in any particular position on the balance.
The blue ball weighs somewhere between 1 and 31 times the weight of a red ball, the ratio being an integer. Enough red balls are placed on the right hand side of the balance to make the beam level. The minimum number of red balls is used to balance any particular weight. There is no restriction on the number of balls in any particular position on the balance.
What is the maximum number of red balls required to balance any blue ball weight within the given range?
Author: Leslie Green
 The picture shows a target that indicates the scores that arrows can make.
The picture shows a target that indicates the scores that arrows can make.
The radiuses of the circles are 3, 5, 7, and 9 units.
If an arrow lands at any point of the target with equal probability, what is the probability to score 9?
 I cut a rectangle into pieces using straight lines, and rearrange these pieces into a hexagon whose sides are all of the same length.
I cut a rectangle into pieces using straight lines, and rearrange these pieces into a hexagon whose sides are all of the same length.
What is the minimum possible number of pieces?
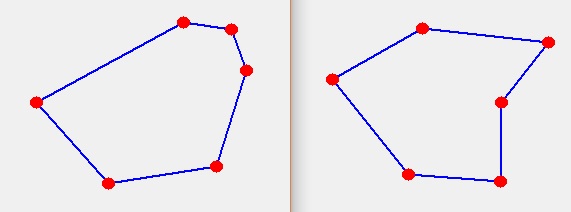 A (simple) polygon is a planar figure composed of non-intersecting line segments (sides) joined into a closed path.
A (simple) polygon is a planar figure composed of non-intersecting line segments (sides) joined into a closed path.
A convex polygon has all internal angles less than 180°.
A concave polygon has at least one internal angle greater than 180°.
The image shows one convex polygon and one concave polygon.
Which statement is true?
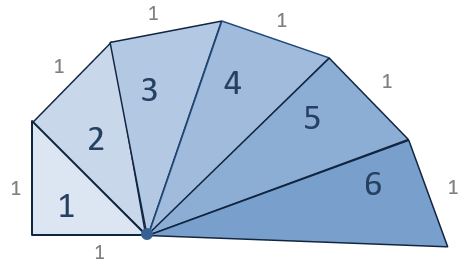 The spiral of Theodorus (also called Pythagorean spiral) is a spiral composed of contiguous right triangles.
The spiral of Theodorus (also called Pythagorean spiral) is a spiral composed of contiguous right triangles.
Which triangle has an area of 1?
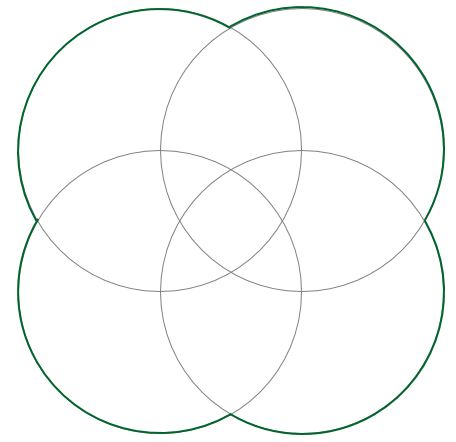 The center of each of the four congruent circles is in the intersection of two other circles.
The center of each of the four congruent circles is in the intersection of two other circles.
If the perimeter of a circle is 6 meters, what is the length of the green external perimeter?
 The picture shows a regular dodecagon, a twelve-sided polygon, covered by equilateral triangles and squares.
The picture shows a regular dodecagon, a twelve-sided polygon, covered by equilateral triangles and squares.
Which area is larger?
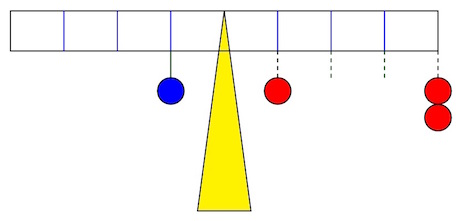
 The skyscraper is 550 meters high, the trees are 50 meters high, and the distance between them is 1km (1,000 meters).
The skyscraper is 550 meters high, the trees are 50 meters high, and the distance between them is 1km (1,000 meters).
Gerry swims towards the trees.At what distance (from the trees) do the trees start to completely hide the skyscraper?
 The three lines are tangent to the inner of the two concentric circles.
The three lines are tangent to the inner of the two concentric circles.
Find the ratio of the circles' diameters.
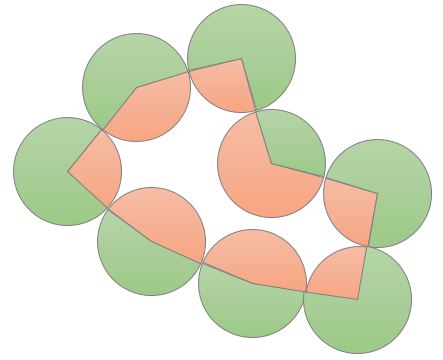 Eight identical circles are externally tangential to one another.
Eight identical circles are externally tangential to one another.
What is the ratio of orange area to green area?
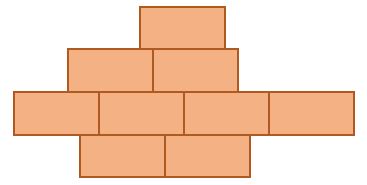 If the perimeter of one of the nine identical rectangles is 12 cm, what is the perimeter of the shape composed from them?
If the perimeter of one of the nine identical rectangles is 12 cm, what is the perimeter of the shape composed from them?
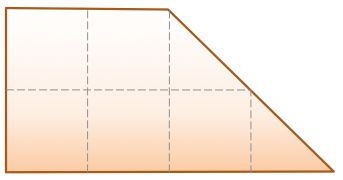
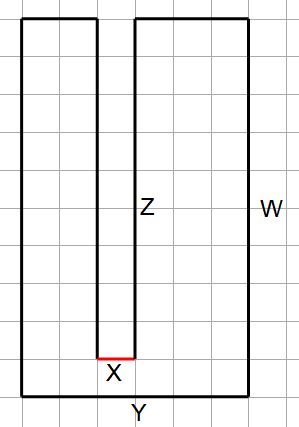 Consider the planar figure shown to the right. All angles are 90°. There are 4 dimensions shown, with X being clearly shown by the red line segment.
Consider the planar figure shown to the right. All angles are 90°. There are 4 dimensions shown, with X being clearly shown by the red line segment.
What is the effect of X on the perimeter of the shape?
Author: Leslie Green
 Leslie Green asks:
Leslie Green asks:
The manufacturer of a particular brand of paint has specified that the 2.5 L of paint in the tin will cover 32 m2.
Neglecting wastage and spillage, how thick is the paint on the wall, assuming the manufacturer's figures are correct?
Note: 1 mL = 1 cm3
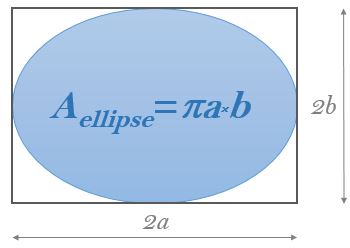 The diagram shows the formula of the area of an ellipse.
The diagram shows the formula of the area of an ellipse.
For what ratio of the length to the width of the rectangle is the percent of its blue area the largest?
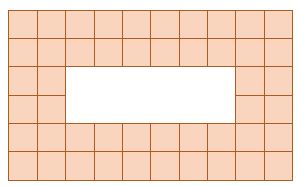 Rearrange the small 1-cm squares, keeping a rectangular shape, but make the outer perimeter as large as possible.
Rearrange the small 1-cm squares, keeping a rectangular shape, but make the outer perimeter as large as possible.
What is the new outer perimeter?