 The scale of a map is 1:20 000.
The scale of a map is 1:20 000.
The distance is measured as 5 centimeters on the map.
How many kilometers is this equivalent to?
Remember:
1 meter = 100 centimeters
1 kilometer = 1000 meters
 The scale of a map is 1:20 000.
The scale of a map is 1:20 000.
The distance is measured as 5 centimeters on the map.
How many kilometers is this equivalent to?
Remember:
1 meter = 100 centimeters
1 kilometer = 1000 meters
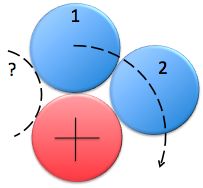 What is the greatest number of circles that can be placed around the central circle?
What is the greatest number of circles that can be placed around the central circle?
They have to touch the central circle. All circles have the same diameter.
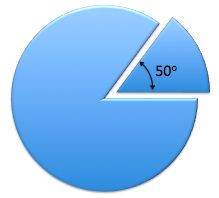 Anna has made puzzle pieces by cutting wedges from a disk.
Anna has made puzzle pieces by cutting wedges from a disk.
Each wedge cut from the disk has a 50-degree angle at the center of the disk.
The weight of the uncut disk is 72 grams.
How many grams does each 50-degree wedge weigh?
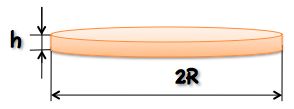 Sixty-four coins are melted down and recast as a single coin of the same thickness h.
Sixty-four coins are melted down and recast as a single coin of the same thickness h.
How many times larger than the diameter of the original coin is the diameter of the new coin?
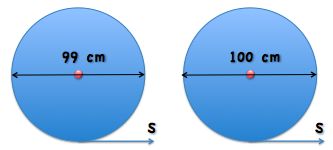 The diameter of the rear wheel of a circus bike is 99 cm. It is 1 cm smaller than the diameter of the front wheel.
The diameter of the rear wheel of a circus bike is 99 cm. It is 1 cm smaller than the diameter of the front wheel.
When the bike goes around the circus, the number of rotations of the smaller wheel is 1 more than the number of rotations of the larger wheel.
Find the number of rotations made by the larger wheel.
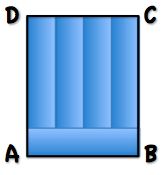 Rectangle ABCD contains five small congruent rectangles. The smaller dimension of one of the small rectangles is 3 cm.
Rectangle ABCD contains five small congruent rectangles. The smaller dimension of one of the small rectangles is 3 cm.
What is the area of rectangle ABCD in square cm?
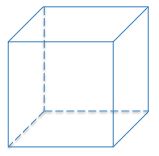 A diagonal is a line joining two non-consecutive vertices of a polygon or polyhedron.
A diagonal is a line joining two non-consecutive vertices of a polygon or polyhedron.
How many different diagonals are in the cube?
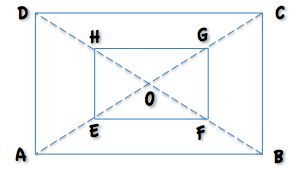 ABCD is a rectangle.
ABCD is a rectangle.
E, F, G and H are midpoints of AO, BO, CO and DO respectively.
What is the fraction of EFGH to ABCD?
Compare the areas.
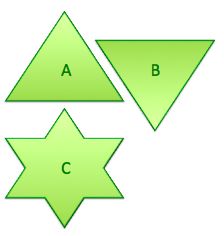 Shape A and B are congruent equilateral triangles.
Shape A and B are congruent equilateral triangles.
Shape C is formed by superimposing shapes A and B by about their centers.
What is the perimeter of shape C if the perimeter of shape A is 36 centimeters?
 The diagram illustrates a row of three squares formed by matches.
The diagram illustrates a row of three squares formed by matches.
How many matches will it take to make a row of 30 squares?
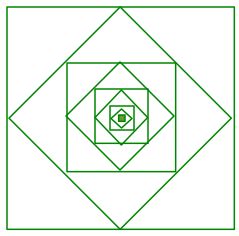 The big square has a side length of 1.
The big square has a side length of 1.
Its sides' midpoints are connected to form a second square, and so forth.
What is the sum of the areas of all the squares in this infinite series?
 A line passes through P(3,1) and Q(36,1000).
A line passes through P(3,1) and Q(36,1000).
How many other points with integer coordinates are on the line and between P and Q?
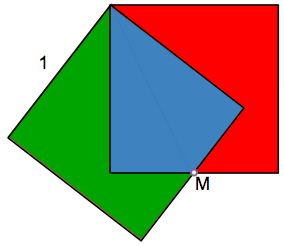 The picture shows two identical squares with sides that have a length of 1 meter.
The picture shows two identical squares with sides that have a length of 1 meter.
M is the midpoint of the corresponding sides of both squares.
What is the area of the blue section?
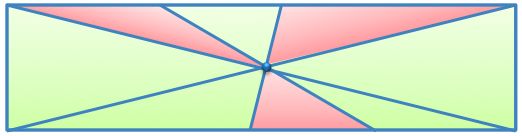 Two lines and two diagonals are drawn through the center of the rectangle.
Two lines and two diagonals are drawn through the center of the rectangle.
What fraction of the area of the rectangle is red?
 In a triangle, the sum of two of the angles is equal to the third.
In a triangle, the sum of two of the angles is equal to the third.
The lengths of the sides are 12,13 and X.
Find X.
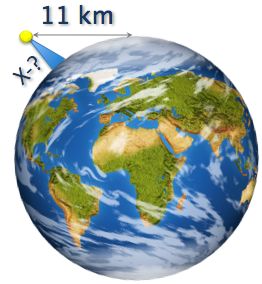 The Earth's diameter is 12,700 km.
The Earth's diameter is 12,700 km.
The horizon is 11 km from the top of a lighthouse.
Estimate the height of the lighthouse.
 How many equilateral triangles can you create using six identical matches?
How many equilateral triangles can you create using six identical matches?
The length of the side of the triangle must be equal to the length of the match.
Source: Fixx, James F Solve It!, 1978
 Four towns are situated at the corners of a square. The government decided to build a new road linking all four towns together. Engineers suggested four different designs.
Four towns are situated at the corners of a square. The government decided to build a new road linking all four towns together. Engineers suggested four different designs.
Which design illustrates the shortest road?
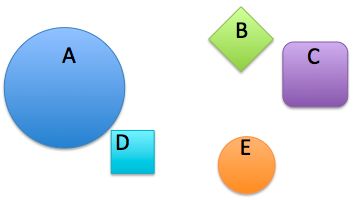 Find two pairs of shapes that are exactly the same distance apart, where the distance between two shapes is defined as the distance between their centers.
Find two pairs of shapes that are exactly the same distance apart, where the distance between two shapes is defined as the distance between their centers.
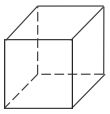 Which of the nets can be folded into a box with a red ribbon printed continuously all the way around it?
Which of the nets can be folded into a box with a red ribbon printed continuously all the way around it?
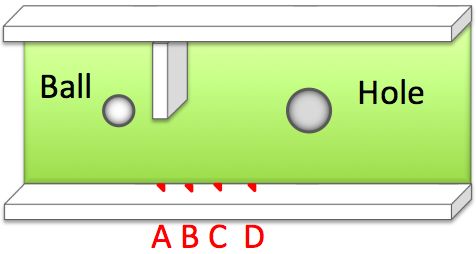 Look at the mini-golf course.
Look at the mini-golf course.
To what point would the player hit the golf ball to make a hole-in-one?
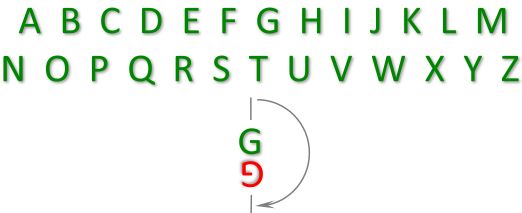 I turned letter G around a center. It no longer reads the same.
I turned letter G around a center. It no longer reads the same.
How many uppercase letters can be read the same after such rotation?
 I use different colors for areas that share a common line segment.
I use different colors for areas that share a common line segment.
What is the least number of colors needed to color the picture?
 You are at point A.
You are at point A.
You can only walk to the north or east.
For example, you can go to point B by two different ways.
How many different ways are there to reach point C?
 Egyptian pyramids are square pyramids.
Egyptian pyramids are square pyramids.
Which of the following nets can be folded to form a square pyramid?
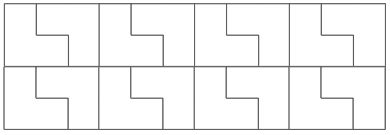
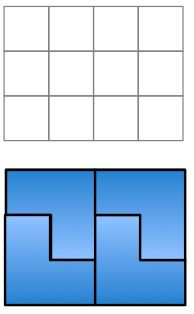 The figure shows an example how a 3x4 net can be covered by L-shaped figures.
The figure shows an example how a 3x4 net can be covered by L-shaped figures.
Which of the figures can be covered by the L-shaped figures in such a manner?
 A telephone company places round cables in round ducts.
A telephone company places round cables in round ducts.
What arrangement of the cables allows the engineers to use a round duct with the smallest diameter?
Remember, there may be more than one correct answer.
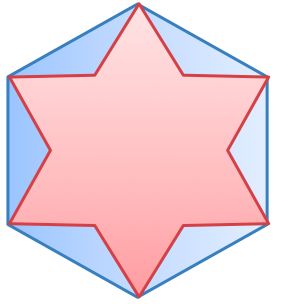 The figure shows a regular hexagon.
The figure shows a regular hexagon.
What is the area of the red part as a fraction of the whole hexagon?
 A point of the square grid is chosen to form an isosceles triangle together with the red segment.
A point of the square grid is chosen to form an isosceles triangle together with the red segment.
How many isosceles triangles can be drawn on the square grid?
 The smallest apple weighs 100 grams.
The smallest apple weighs 100 grams.
The largest apple has a perimeter 10% larger than that of the smallest apple.
Estimate the weight of the largest apple.
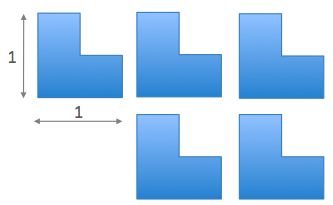 I want to place together five identical shapes without overlapping them to form a figure.
I want to place together five identical shapes without overlapping them to form a figure.
What is the least perimeter of the figure?
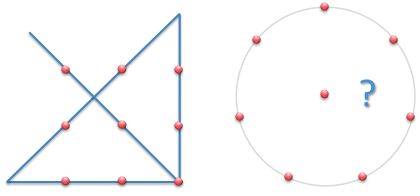 The left picture shows nine dots arranged in a 3 x 3 square.
The left picture shows nine dots arranged in a 3 x 3 square.
The dots are connected using only four straight lines and without lifting the pen from the paper.
The right picture shows seven dots evenly distributed on a circle and a dot in the center.
How many straight lines connect the dots in the same way?
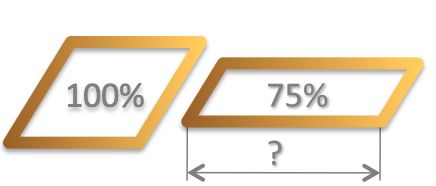 Anna takes a rope that is 16 meters long and creates a square.
Anna takes a rope that is 16 meters long and creates a square.
Bob takes the rope and creates a rectangle that has an area 75% of the square's area.
What is the length of the rectangle?
 Which of these diagrams could be drawn completely without lifting the pen off the paper or going over any line twice?
Which of these diagrams could be drawn completely without lifting the pen off the paper or going over any line twice?
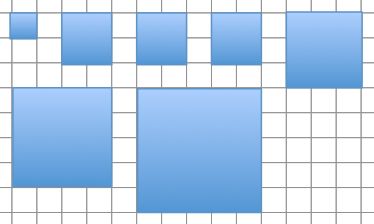 Seven squares with side length of 1, 2, 2, 2, 3, 4, and 5 units can be fitted together with no gaps and no overlaps, to form a rectangle.
Seven squares with side length of 1, 2, 2, 2, 3, 4, and 5 units can be fitted together with no gaps and no overlaps, to form a rectangle.
What is the length of the shorter side of the rectangle?
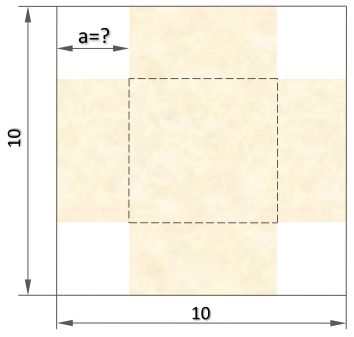
 The area of the white cross is 20% of the area of the square flag.
The area of the white cross is 20% of the area of the square flag.
Five white squares form the cross.
What is the length of the side of the white square?
 Two heights in a triangle are both not less than either of two of its sides.
Two heights in a triangle are both not less than either of two of its sides.
Find the largest angle.
 A Heronian triangle is a triangle whose side lengths and area are all integer numbers.
A Heronian triangle is a triangle whose side lengths and area are all integer numbers.
It is named after Hero of Alexandria.
Find sizes of a triangle whose area is numerically the same as its perimeter.
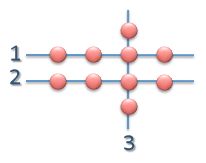 I arrange 10 points so that 3 lines each go through 4 points.
I arrange 10 points so that 3 lines each go through 4 points.
I would like to rearrange these 10 points.
What is the greatest number of lines that go through 4 dots each?
 The top of a rectangular box has an area of 20 square meters, and two sides have areas of 12 and 15 square meters.
The top of a rectangular box has an area of 20 square meters, and two sides have areas of 12 and 15 square meters.
What is the volume of the box?
 What is the probability that a point chosen randomly from the interior of an equilateral triangle is closer to a vertex of the triangle than it is to a midpoint of one of the triangle's sides?
What is the probability that a point chosen randomly from the interior of an equilateral triangle is closer to a vertex of the triangle than it is to a midpoint of one of the triangle's sides?
 This shape was formed by removing a small cube from a big cube.
This shape was formed by removing a small cube from a big cube.
The side length of the removed cube is two thirds of the side length of the original cube.
What is the volume of the new shape compared with the original volume?
 I want to cut a wooden cube that is four inches on each side into 64 one-inch cubes.
I want to cut a wooden cube that is four inches on each side into 64 one-inch cubes.
I can do this by making 3 + 3 + 3 = 9 cuts, keeping the pieces together in the cube shape.
What is the minimum number of cuts needed if rearrangement of the pieces after each cut is allowed?
 What is the probability that a point chosen randomly from the interior of a circle is closer to the circle's center than it is to any point of the circle's circumference?
What is the probability that a point chosen randomly from the interior of a circle is closer to the circle's center than it is to any point of the circle's circumference?
 A rectangle has a width of 0.7x and a length of 0.4x.
A rectangle has a width of 0.7x and a length of 0.4x.
Which formula is the correct one to calculate the perimeter (P) in terms of x?
 A boy is making boxes from cardboard.
A boy is making boxes from cardboard.
He is going to cut square pieces off each corner as shown in the diagram and fold the sides up.
Which size of square pieces would give a larger box in terms of volume?
 The American flag consists of thirteen equally spaced, horizontal red and white stripes, with a blue rectangle in the canton bearing fifty small, white, five-pointed stars.
The American flag consists of thirteen equally spaced, horizontal red and white stripes, with a blue rectangle in the canton bearing fifty small, white, five-pointed stars.
What part of the flag is white stripes?
 A block of wood in the form of a cuboid 8 x 9 x 10 has all its six faces painted red.
A block of wood in the form of a cuboid 8 x 9 x 10 has all its six faces painted red.
If the wooden block is cut into small cubes of 1 x 1 x 1, how many of these cubes would have red paint on them?
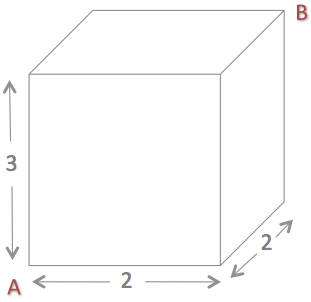 A bug walks from corner A of a room to corner B by only moving along the walls.
A bug walks from corner A of a room to corner B by only moving along the walls.
What is the shortest path it can take?
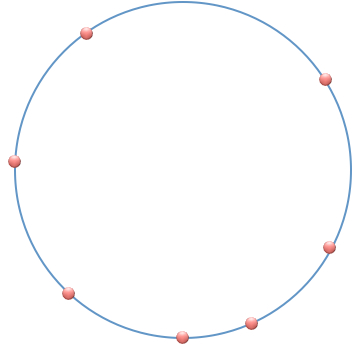 Connect 7 points on the circumference of a circle.
Connect 7 points on the circumference of a circle.
What is the largest number of intersections for the chords?
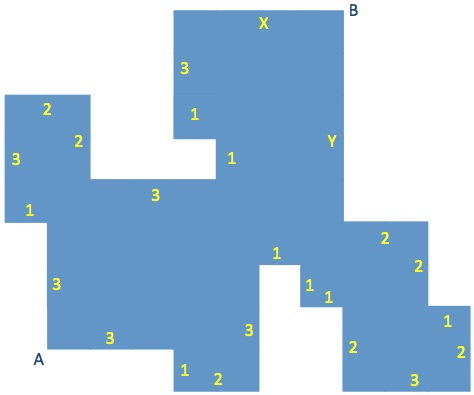 All angles are right and the lengths of the sides are given in miles in the diagram.
All angles are right and the lengths of the sides are given in miles in the diagram.
Find the length of the shortest path from A to B along the sides of the shape.
 In a triangle, the sum of two of the angles is equal to the third, and the lengths of the two longer sides are 25 and 24.
In a triangle, the sum of two of the angles is equal to the third, and the lengths of the two longer sides are 25 and 24.
What is the length of the shortest side?
 What is the absolute difference between the largest and smallest possible perimeters of two rectangles that each have an area of 100 square units and integer side lengths?
What is the absolute difference between the largest and smallest possible perimeters of two rectangles that each have an area of 100 square units and integer side lengths?
 An aquarium has a water surface area of 10,000 cm2.
An aquarium has a water surface area of 10,000 cm2.
I put a brick that measures 40 cm x 20 cm x 12.5 cm in the aquarium.
Estimate by how many centimeters the water rises.
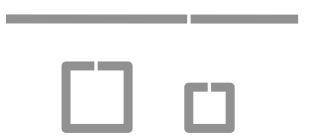 A piece of wire 75 cm in length is cut into two parts, one of them being 30 cm long.
A piece of wire 75 cm in length is cut into two parts, one of them being 30 cm long.
Each part is bent to form a square.
What is the ratio of the area of the larger square to the smaller square?
 A 3 by 4 rectangle is contained within a circle.
A 3 by 4 rectangle is contained within a circle.
What is the smallest possible diameter of the circle?
This is typical SAT question.
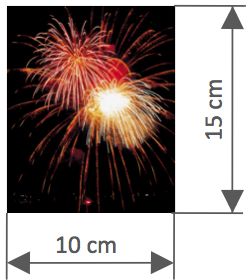 A photograph is placed in a frame that forms a border 2.5 cm wide on all sides of the photograph.
A photograph is placed in a frame that forms a border 2.5 cm wide on all sides of the photograph.
What is the area of the border?
 I have 33 coins.
I have 33 coins.
What is the minimum number of coins I need in order to make sure that each coin touches exactly three other coins?
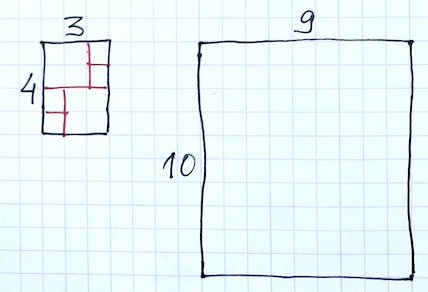 I divided a 3 x 4 square into 6 squares.
I divided a 3 x 4 square into 6 squares.
What is the smallest number of squares into which you can divide a 9 x 10 rectangle?
Author: Matt Enlow
 A wooden empty box weighs 80 pounds.
A wooden empty box weighs 80 pounds.
How much will another box of the same material weigh if its sides are twice as long?
 The picture shows a polygon with 7 sides and 5 right angles.
The picture shows a polygon with 7 sides and 5 right angles.
How many interior right angles are possible in a polygon with eight sides?
 There are 17 parallels and 12 meridians on a globe.
There are 17 parallels and 12 meridians on a globe.
Into how many areas is the surface of the globe divided?
 What is the difference between the red area and the blue area if the numbers show the side lengths of each square?
What is the difference between the red area and the blue area if the numbers show the side lengths of each square?
 Swiss village Saas-Fee is entirely pedestrian and serviced by electric taxis and buses only. All electricity is obtained from 100% renewable hydroelectric power. The people have equipped the community's 250 wood-fired furnaces with particle filters.
Swiss village Saas-Fee is entirely pedestrian and serviced by electric taxis and buses only. All electricity is obtained from 100% renewable hydroelectric power. The people have equipped the community's 250 wood-fired furnaces with particle filters.
Design guidelines for the village require houses to be 40% wooden, to maintain its architectural character. Its area is about 40 km2.
If the border of the village was a circle what would be the maximum distance an electric car goes to cross the entire village?
 The sum of the perimeters of three rectangles is 172cm.
The sum of the perimeters of three rectangles is 172cm.
What is the largest possible sum of their areas?
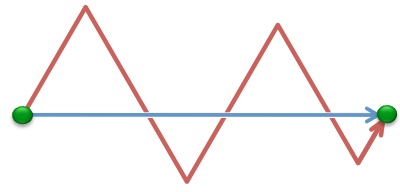 Gerry frequently goes from his home to Jane's house, which is 4 miles away.
Gerry frequently goes from his home to Jane's house, which is 4 miles away.
He chooses the straight (blue) path on Monday and a red path with the form of equilaterial triangles on Tuesday.
How much longer is the second path?
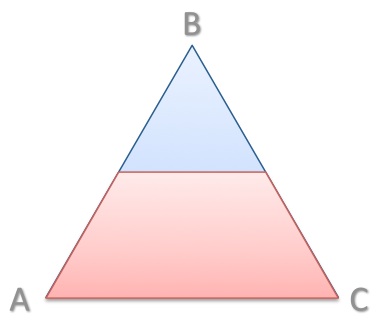 Triangle ABC is equilateral.
Triangle ABC is equilateral.
What is the ratio of the red and blue areas if the heights of the blue triangle and the red trapezoid are the same?
 A team of archaeologists is exploring an underground complex on a remote planet. On each level there is a regular grid of North-South corridors intersecting East-West corridors, with ladders at each junction going both up and down to the next levels. Effectively the complex appears to be a regular 3D lattice of tunnels.
A team of archaeologists is exploring an underground complex on a remote planet. On each level there is a regular grid of North-South corridors intersecting East-West corridors, with ladders at each junction going both up and down to the next levels. Effectively the complex appears to be a regular 3D lattice of tunnels.
The previous team has marked the tunnels and made a list of problematic junctions that need to be avoided.
The team is currently at junction (3, 2, 5) and needs to get to junction (12, 9, 8) by one of the many shortest available routes.
Which of the listed problematic junctions might be in their way?
Author: Leslie Green
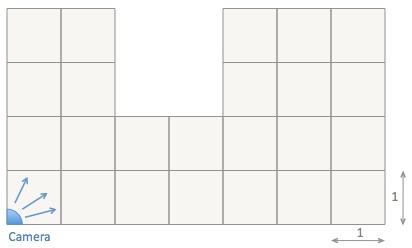 A shop owner installs a security camera on the ceiling of his shop. The camera can turn up-down and right round through 360°. The picture shows the design of the shop.
A shop owner installs a security camera on the ceiling of his shop. The camera can turn up-down and right round through 360°. The picture shows the design of the shop.
What part of the shop floor is hidden from the camera?
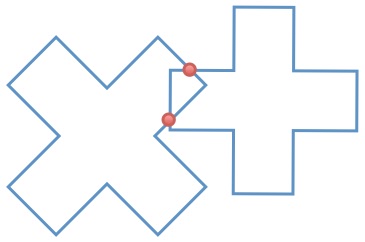 In the diagram, two crosses intersect at exactly two points.
In the diagram, two crosses intersect at exactly two points.
What is the maximum possible number of points of intersection of any two crosses of the same size?
 What is the ratio of the white area to the blue area if the radius of the small semicircles is 4 times smaller than the large one?
What is the ratio of the white area to the blue area if the radius of the small semicircles is 4 times smaller than the large one?
 A cellar floor is to be tiled in the way shown in the picture.
A cellar floor is to be tiled in the way shown in the picture.
If the cellar measures 25 tiles x 27 tiles, how many white tiles will be needed?
 Hydraulic pumps pump cleaned water from a filled tank into a special pond via tubes that have an input diameter of 16 cm and an output diameter of 8 cm.
Hydraulic pumps pump cleaned water from a filled tank into a special pond via tubes that have an input diameter of 16 cm and an output diameter of 8 cm.
How much faster does the water go through the output outlet compared to the input tube?
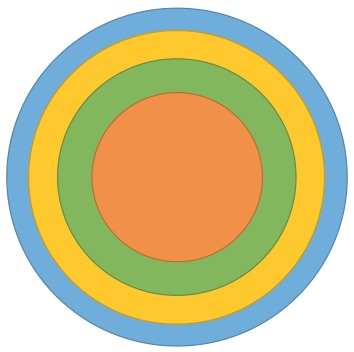 All the circles have the same center. The area of each colored region between the circles is equal to the area of the smaller circle.
All the circles have the same center. The area of each colored region between the circles is equal to the area of the smaller circle.
How much larger is the largest circle compared to the small circle?
 A shape is made from 6 congruent equilateral triangles that share one, two, or three common sides.
A shape is made from 6 congruent equilateral triangles that share one, two, or three common sides.
What is the maximum possible number of sides the shape has?
 Egyptians used a 12-unit-length rope with 2 knots to form a right triangle. They used the triangle to define the right angle when they divided the land.
Egyptians used a 12-unit-length rope with 2 knots to form a right triangle. They used the triangle to define the right angle when they divided the land.
What are the rope's segment lengths?
 The picture shows two circles with diameters of length 1 and 4, which have the same centre.
The picture shows two circles with diameters of length 1 and 4, which have the same centre.
What fraction of the larger circle is blue?
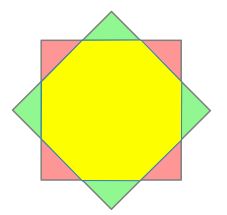 The design is formed by 2 squares of area of 9 square metres that has the same center.
The design is formed by 2 squares of area of 9 square metres that has the same center.
Find the area of the yellow shape.
 Flying Superman stands 40 feet away from a tree that is 9 feet tall. He has to get to the top of the tree to save Jane's kitten.
Flying Superman stands 40 feet away from a tree that is 9 feet tall. He has to get to the top of the tree to save Jane's kitten.
How far will he have to travel straight to the kitten and to fall down under the tree?
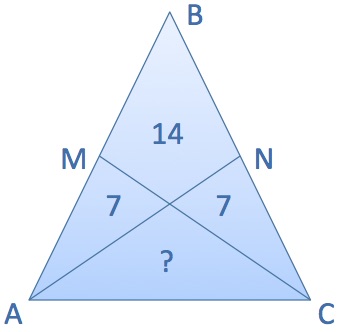 The picture shows an isosceles triangle ABC. M and N are midpoints of the corresponding sides. The numbers show the areas of three parts of the triangle.
The picture shows an isosceles triangle ABC. M and N are midpoints of the corresponding sides. The numbers show the areas of three parts of the triangle.
What is the area of the fourth region?
 If a pizza has radius Z and height A, what is the volume of the meal?
If a pizza has radius Z and height A, what is the volume of the meal?
The number &π (PI) is a mathematical constant, the ratio of a circle's circumference to its diameter, commonly approximated as 3.14159.
 The basketball hoop is 45.7cm in diameter, and 3.05m high. The basketball is 24cm in diameter.
The basketball hoop is 45.7cm in diameter, and 3.05m high. The basketball is 24cm in diameter.
Compare the cross-sectional area of the ball with the area of the hoop.
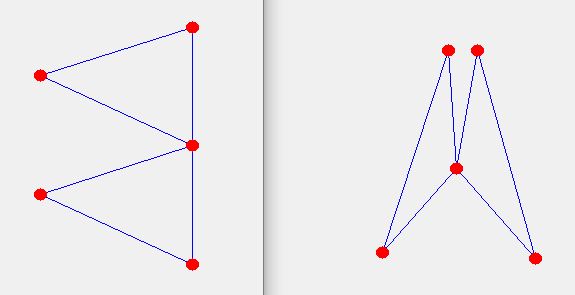 Pretend the round red blobs are tennis balls. Pretend the blue lines are stretchy strings.
Pretend the round red blobs are tennis balls. Pretend the blue lines are stretchy strings.
Can you move the tennis balls from the pattern on the left to make the pattern on the right?
NOTE: the strings are special so that whatever you do they never get tangled up with each other.
Author: Leslie Green
 Pretend the round red blobs are tennis balls. Pretend the blue lines are stretchy strings.
Pretend the round red blobs are tennis balls. Pretend the blue lines are stretchy strings.
Can you move the tennis balls from the pattern on the left to make the pattern on the right?
NOTE: the strings are special so that whatever you do they never get tangled up with each other.
Author: Leslie Green
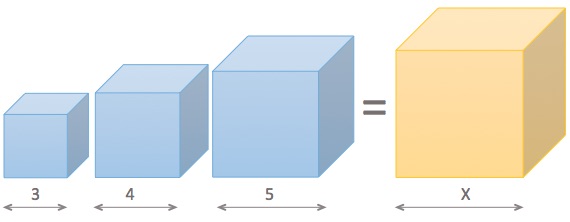 Gerry wants to replace three cube-shaped reservoirs with side lengths of 3, 4, and 5 meters by a large reservoir with the same volume.
Gerry wants to replace three cube-shaped reservoirs with side lengths of 3, 4, and 5 meters by a large reservoir with the same volume.
What is the side length of the new reservoir?
 A circle is divided into four identical regions by the four semicircles.
A circle is divided into four identical regions by the four semicircles.
Compare the perimeter of a shape with the perimeter of the circle?
 If the radius of the large circle is 7,
If the radius of the large circle is 7,
the radius of the green circle is 1, and
the red and yellow areas are equal,
what is the external radius of the yellow ring?
 I cut a rectangle into pieces using straight lines, and rearrange these pieces into a hexagon whose sides are all of the same length.
I cut a rectangle into pieces using straight lines, and rearrange these pieces into a hexagon whose sides are all of the same length.
What is the minimum possible number of cuts?
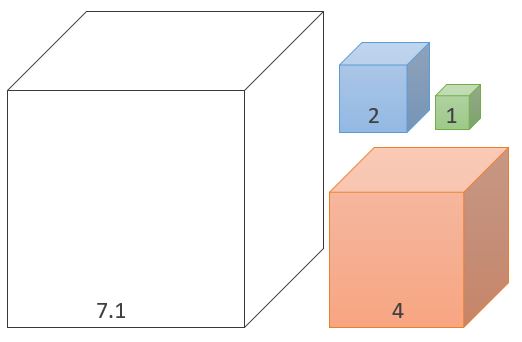 Gerry has an empty box with side lengths of 7.1 meters, and an unlimited number of cubes with side lengths of 4, 2, and 1 meters.
Gerry has an empty box with side lengths of 7.1 meters, and an unlimited number of cubes with side lengths of 4, 2, and 1 meters.
What is the minimum number of cubes needed to fill the box to its maximum extent?
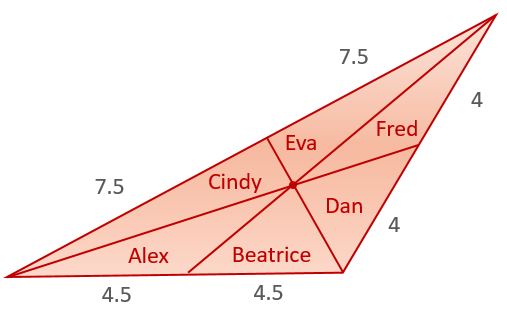 Alex shares a triangular piece of cake between 5 friends and himself.
Alex shares a triangular piece of cake between 5 friends and himself.
The numbers show the lengths of corresponding segments in inches.
Who gets the heaviest piece?
 Ugg, the primitive human, finds a perfectly circular fountain with a diameter of 1.8m. Of course Ugg doesn't know what a fountain is, or what a diameter is, but he decides to measure the circumference of the fountain, despite not knowing what a circumference actually is. Ugg can only measure using his walking stick and a piece of chalk. The walking stick is remarkably straight, and by sheer chance it just happens to be exactly 1m long.
Ugg, the primitive human, finds a perfectly circular fountain with a diameter of 1.8m. Of course Ugg doesn't know what a fountain is, or what a diameter is, but he decides to measure the circumference of the fountain, despite not knowing what a circumference actually is. Ugg can only measure using his walking stick and a piece of chalk. The walking stick is remarkably straight, and by sheer chance it just happens to be exactly 1m long.
Ugg is not as clever as you, so he would not think of pressing the stick against the curve and moving the pressure point down the length of the stick to follow the curve exactly.
What is Ugg's count of the number of sticks needed to surround the strange looking historic artefact he has found?
Unusually, and just for this question, you are encouraged to open another browser tab and search for any information on the Internet which will help you to solve this problem.
Author: Leslie Green
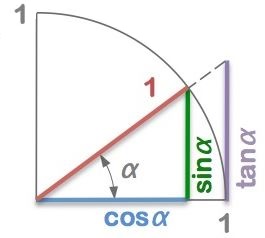 Leslie Green asks:
Leslie Green asks:
The sine of an angle, A, is identically equal to the cosine of some other angle.
What is the other angle?
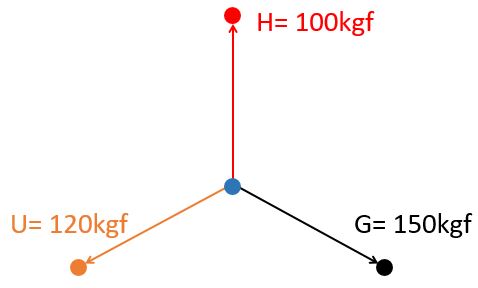 Today there is a tug of war between a human, an orangutan, and a gorilla. You may be unfamiliar with the units being used. We call the force necessary to support a 1kg weight one kilogram-force, with the notation 1kgf. Whilst this is not one of the preferred SI units, it is easy to understand from everyday experience.
Today there is a tug of war between a human, an orangutan, and a gorilla. You may be unfamiliar with the units being used. We call the force necessary to support a 1kg weight one kilogram-force, with the notation 1kgf. Whilst this is not one of the preferred SI units, it is easy to understand from everyday experience.
The human pulls in the compass direction of 000° with a strength of 100kgf. The orangutan thinks it is very funny and pulls with a force of 120kgf in the compass direction of 240°. The gorilla really can't be bothered, so only pulls with a force of 150kgf in the compass direction of 120°.
In which compass direction does the junction of the ropes move?
Author: Leslie Green
 Shawna wishes to measure the height of a tree for no clearly explained reason. She has determined that the distance from the ground to her eye level is 1.7m when she is wearing her usual fashionable boots. She uses a 45° set-square to sight-along and she uses a spirit level to make sure the ground is level and the base of the set-square is also level.
Shawna wishes to measure the height of a tree for no clearly explained reason. She has determined that the distance from the ground to her eye level is 1.7m when she is wearing her usual fashionable boots. She uses a 45° set-square to sight-along and she uses a spirit level to make sure the ground is level and the base of the set-square is also level.
She walks back from the tree until the top of the tree aligns with the set square, then she measures the distance from where she is standing to the centre of the tree trunk. The distance she measures is 11.2m.
What is her estimate of the height of the tree?
Author: Leslie Green
 An equilateral polygon can be concave. It can also have a rotational symmetry. For example, the star is a concave decagon (ten-side polygon) with rotational symmetry.
An equilateral polygon can be concave. It can also have a rotational symmetry. For example, the star is a concave decagon (ten-side polygon) with rotational symmetry.
What is the least number of sides a concave equilateral polygon with rotational symmetry can have?
Definition: A concave polygon has at least one internal angle greater than 180°.
Definition: An equilateral polygon has all sides of equal length.
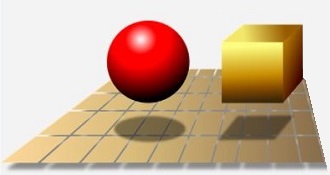 Examine the following statements:
Examine the following statements:
1) For a given stored volume, a sphere has less surface area than a cube.
2) For a given width limit, a sphere and a cube have the same ratio of volume to surface area.
3) A cube of a given width will have a lower volume to surface area ratio than a cuboid of the same dimensions (except its length is twice its width).
Author: Leslie Green
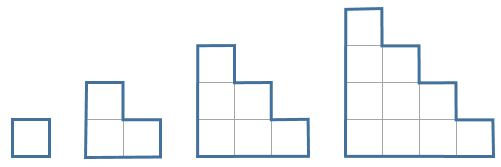 We form shapes with squares 1 cm high.
We form shapes with squares 1 cm high.
The first four stages of a sequence are shown in the picture.
What is the area of the stage 111 in the sequence?
 Leslie Green asks:
Leslie Green asks:
The super-villain of a science-fiction movie shrinks the moon to one hundredth of its original diameter.
If we willingly suspend our disbelief for a moment, and we of course assume that the Law of Conservation of Mass applies, what is the resulting average density of the shrunken moon?
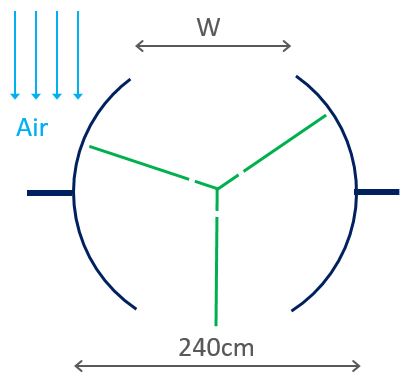 A revolving door prevents circulation of the external air inside a building.
A revolving door prevents circulation of the external air inside a building.
What is the largest possible width W for the design?
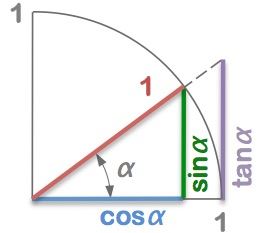 What are the units of arctan?
What are the units of arctan?
(arctan is also written as atan and tan raised to the power -1 : tan-1)
 A hill has the characteristic that for every 2 cubits of real horizontal motion there is one cubit of real vertical motion.
A hill has the characteristic that for every 2 cubits of real horizontal motion there is one cubit of real vertical motion.
What is the angle of the slope relative to the horizontal?
NOTE: Inverse trig functions can be written with an arc- prefix, an a- prefix, or be raised to the power -1.
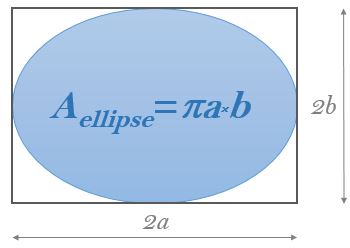 The diagram shows the formula of the area of an ellipse.
The diagram shows the formula of the area of an ellipse.
What percent of the area of the rectangle is blue?
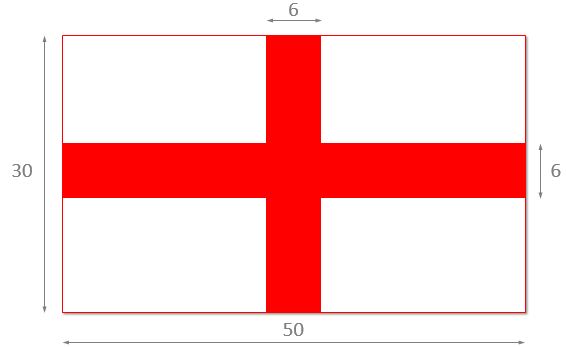 The flag of England is derived from St George's Cross. The official proportions for the national flag of England is 3:5, with the cross being 1/5 of the height of the flag wide. The picture shows an example of the dimensions of the flag.
The flag of England is derived from St George's Cross. The official proportions for the national flag of England is 3:5, with the cross being 1/5 of the height of the flag wide. The picture shows an example of the dimensions of the flag.
Estimate the area of the red part of the flag.
 The measure of the two acute angles in a right triangle are in the ratio 5:13.
The measure of the two acute angles in a right triangle are in the ratio 5:13.
What is the measure of the smallest angle of the triangle?